|
| Foro Departamento de Matemática Teóricos Función |
| Función |
|
06-09-2013, 10:59 PM
Post: #1
|
|||
|
|||
|
Función
Toda función es una relación entre dos conjuntos. Se suele distinguir entre el conjunto de partida y el de llegada. Una función lo que hace es asignar a cada elemento del conjunto de partida un único elemento del conjunto de llegada. En matemática, utilizamos las llamadas expresiones matemática, valga la redundancia, que son expresiones algebraicas: conjunto de números y letras, unidos por operadores matemáticos, tales como: suma, resta, división, multiplicación, entre otros. Cuando hablamos de una función, denotamos a esta colocando previo a la expresión, lo siguiente: "\( f(x) \)". La letra \( f \) puede ser cambiada por cualquier otra letra del alfabeto latino, siempre y cuando, no sea \( x \) ni \( y \). La expresión matemática a la que hice referencia en una primera instancia, sólo puede presentar un variable, pero esta puede estar repetida varias veces y de diferentes formas. Es conveniente llamar \( x \) a esta variable. Una función, por ejemplo, es la siguiente: $$ f(x) = x^2 - 4 $$ Como dije anteriormente, una función "asigna a cada elemento del conjunto de partida un único elemento del conjunto de llegada". Esto significa que para cada valor que yo le doy a la variable dependiente \( x \), habrá un único valor que le corresponda a \( f(x) \). Esto lo podemos de ver de la siguiente forma: 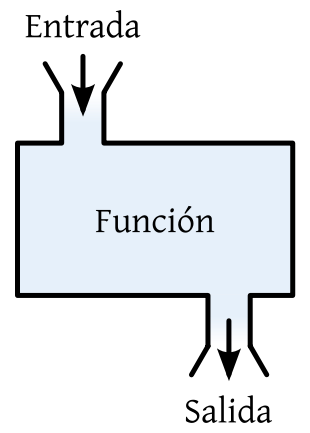 Un ejemplo, para entender más: Si tengo una función: \( f(x) = x^2 - 4 \), y sustituyo \( x = 1 \), tendré la siguiente expresión: \( f(1) = (1)^2 - 4 = -3 \). Esto quiere decir que para el elemento "1" del conjunto de partida, le corresponde el elemento "-3" del conjunto de llegada. Para facilitar aún más el estudio de las funciones, se inventó, lo que hoy comúnmente se conoce como gráfico. Los conceptos de funciones, que permitieron la geometría analítica, fueron resultado de los grandes aportes del matemático francés René Descartes. El análisis de las funciones, constituye gran parte de los estudios terciarios en matemática, debido a su complejidad, a causa su abstracción. Dicho de una forma más formal, podemos afirmar lo siguiente: Cita Definición de función: Si cada uno de los elementos de A se relaciona con un y sólo un elemento de B, entonces f es una función de A en B. Expresado en lenguaje matemático: $$ f:A→B $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-09-2013, 11:28 PM
Post: #2
|
|||
|
|||
|
Clasificación:
· Función inyectiva: una función es inyectiva si a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Pueden quedar elementos sin correspondencia en el segundo conjunto, como se muestra en la imagen. 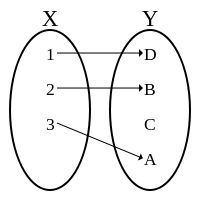 · Función sobreyectiva: una función es sobreyectiva si no hay ningún elemento del primer conjunto sin correspondencia en el segundo. 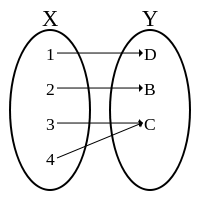 · Función biyectiva: es aquella función que es inyectiva y sobreyectiva al mismo tiempo, o sea, a cada elemento del primero conjunto le corresponde un elemento del segundo que es único y ningún elemento queda sin correspondencia. 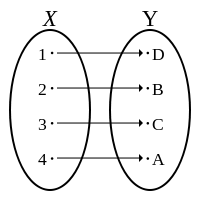 · Función inversa: denotada como \( f^{-1} \), cumple que si \( f(A) = B ⇒ f^{-1}(B) = A \). · Función compuesta: 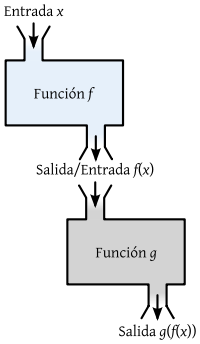 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-09-2013, 11:36 PM
Post: #3
|
|||
|
|||
|
Conceptos generales de una función:
· Dominio: es el conjunto de todos los valores de abscisa en los que existe la función. · Codominio: es el conjunto de todos los valores de ordenada en los que existe la función. · Raíces: una raíz es el corte del gráfico con el eje \( O \vec x \). Se pueden calcular analíticamente, igualando la expresión a cero y despejando la variable. · Ordenada en el origen: una ordenada en el origen es el corte del gráfico con el eje \( O \vec y \). Se pueden calcular analíticamente, mediante la sustitución numérica \( f(0) \). Visto de otra forma, el término independiente de la expresión, es la ordenada en el origen de la función. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-09-2013, 11:50 PM
Post: #4
|
|||
|
|||
|
Tipos de funciones:
· Función constante: Toda función constante es de la forma: $$ f(x) = a, a∈ℝ $$ · Función polinómica: Toda función polinómica es de la forma: $$ f(x) = \sum_{i=0}^{i=n} (a_{i}·x^{i}) = a_{n}·x^{n} + a_{n-1}·x^{n-1} + ... + a_{1}·x + a_{0} $$ Este tipo de funciones ha sido ampliamente estudiado a través de la historia, debido a que la mayoría de los problemas de la realidad, se reducen a ellas. · Función racional: Toda función racional es de la forma: $$ f(x) = \frac {p(x)}{q(x)} $$ Condición de existencia: \( g(x) ≠ 0 \) · Función exponencial: Toda función exponencial es de la forma: $$ f(x) = a^{p(x)} $$ · Función logarítmica: Toda función logarítmica es de la forma: $$ f(x) = \log_{a} (p(x)) $$ Condición de existencia: \( p(x) > 0 \) · Función radical: Toda función radical es de la forma: $$ f(x) = \sqrt [a]{p(x)} $$ Si se trata de una raíz de índice par: Condición de existencia: \( p(x) > 0 \) · Función módulo o función valor absoluto: Toda función módulo es de la forma: $$ f(x) = |p(x)| $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-09-2013, 11:51 PM
Post: #5
|
|||
|
|||
|
Asíntotas de una función
Definición: Una asíntota es una recta, a la cual se acerca infinitamente la función. Existen tres tipos de asíntotas. Tipos de asíntotas: · Asíntota vertical: Existe una asíntota en \( x = a \) si y sólo si al menos uno de los límites laterales de cuando \( x \to a \) es infinito. · Asíntota horizontal: Existe una asíntota en \( y = a \) si y sólo si al menos uno de los límites cuando \( x \to ∞ \) es un número finito \( a \). · Asíntota oblicua: Existe una asíntota oblicua de ecuación \( y = m·x+n \) si y sólo si al menos uno de los límites cuando \( x \to ∞ \) es \( ∞ \). Cálculo de la asíntota oblicua de ecuación \( y = m·x + n \): · Cálculo de \( m \): $$ \lim_{x \to ∞} \frac {f(x)}{x} = m $$ · Cálculo de \( n \): $$ \lim_{x \to ∞} (f(x) - m·x) = n $$ · Saber más sobre asíntotas de una función. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-09-2013, 11:52 PM
Post: #6
|
|||
|
|||
|
Continuidad:
· Continuidad de una función en un punto de ella: Una función \( f \) es continua en \( x = a \) si y sólo si se cumplen las siguientes condiciones: $$ ∃ f(a) $$ $$ ∃ \lim_{x \to a} f(x) $$ $$ \lim_{x \to a} f(x) = f(a) $$ · Continuidad de una función en un intervalo de ella: \( f \) es continua en \( [a,b] \) si y sólo si se cumplen las siguientes condiciones: \( f \) es continua \( ∀x,x∈(a,b) \) \( f \) es continua en \( b^{-} \) \( f \) es continua en \( a^{+} \) · Continuidad de una función en el lateral de un punto de ella: \( f \) es continua en \( a^{+} \) si y sólo si se cumple la siguiente condición: $$ \lim_{x \to a^{+}} f(x) = f(a) $$ \( f \) es continua en \( a^{-} \) si y sólo si se cumple la siguiente condición: $$ \lim_{x \to a^{-}} f(x) = f(a) $$ Teoremas sobre continuidad: · Teorema de Bolzano: si una función \( f(x) \) es continua en un intervalo \( [a,b] \) y se cumple la condición de que \( f(a) \) y \( f(b) \) son de distinto signo, entonces, podemos afirmar que existe al menos una raíz dentro de dicho intervalo. Leer más. · Teorema de Darboux: si una función es continua en el intervalo \( [a, b] \) y \( k \) es un número comprendido entre los valores \( f(a) \) y \( f(b) \), entonces existe al menos un \( c∈(a, b) \) tal que \( f( c ) = k \). Leer más. · Teorema de Weierstrass: si una función \( f(x) \) está definida y es continua en un intervalo \( [a, b] \), entonces \( f(x) \) alcanza al menos un máximo y un mínimo absolutos en el intervalo \( [a, b] \). Leer más. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
07-09-2013, 0:02 AM
Post: #7
|
|||
|
|||
|
Funciones crecientes, decrecientes y constantes:
· Función estrictamente creciente dentro de un intervalo: Una función es estrictamente creciente en un intervalo \( (a, b) \) si y sólo si para dos valores cualesquiera \( x_{1} \) y \( x_{2} \) del intervalo, se cumple que: $$ \frac{f(x_2)-f(x_1)}{x_{2}-x_{1}} > 0 $$ · Función creciente dentro de un intervalo: Una función es creciente en un intervalo \( (a, b) \) si y sólo si para dos valores cualesquiera \( x_{1} \) y \( x_{2} \) del intervalo, se cumple que: $$ \frac{f(x_2)-f(x_1)}{x_{2}-x_{1}} ≥ 0 $$ · Función estrictamente decreciente dentro de un intervalo: Una función es estrictamente decreciente en un intervalo \( (a, b) \) si y sólo si para dos valores cualesquiera \( x_{1} \) y \( x_{2} \) del intervalo, se cumple que: $$ \frac{f(x_2)-f(x_1)}{x_{2}-x_{1}} < 0 $$ · Función decreciente dentro de un intervalo: Una función es decreciente en un intervalo \( (a, b) \) si y sólo si para dos valores cualesquiera \( x_{1} \) y \( x_{2} \) del intervalo, se cumple que: $$ \frac{f(x_2)-f(x_1)}{x_{2}-x_{1}} ≤ 0 $$ · Función constante dentro de un intervalo: Una función es constante en un intervalo \( (a, b) \) si y sólo si para dos valores cualesquiera \( x_{1} \) y \( x_{2} \) del intervalo, se cumple que: $$ \frac{f(x_2)-f(x_1)}{x_{2}-x_{1}} = 0 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
08-09-2013, 11:13 PM
Post: #8
|
|||
|
|||
|
Límite de una función
El límite de una función, permite conocer los valores de tendencia de ordenada para los valores elegidos de abscisa. En definitiva, permite conocer qué sucede con una función cuando la abscisa toma valores muy chicos o muy grandes, o incluso sirve para cuando no se puede hacer el valor numérico \( f(a) \). La notación que se utiliza es: $$ \lim_{x \to a} f(x) = b $$ Es una herramienta muy útil a la hora de graficar. Además que gracias a los límites, podemos calcular las asíntotas. · Aprender más sobre límites. · Cómo calcular límites. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
28-11-2013, 9:16 PM
Post: #9
|
|||
|
|||
|
Derivada
La derivada nos permite conocer la pendiente de cualquier punto de la función. Se dice que es el valor de la recta tangente en cualquier punto. Derivada de una función en un punto de ella $$ f'(a) = \lim_{x \to a} \frac {f(x) - f(a)}{x - a} $$ Derivada de una función $$ f'(x) = \lim_{h \to 0} \frac {f(x+h) - f(x)}{h} $$ Gracias a esto, podremos saber dónde y hay máximos y mínimos (pendiente nula). · Aprender mucho más. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |







