|
| Foro Departamento de Matemática Teóricos Derivada |
| Derivada |
|
25-07-2013, 8:12 PM
Post: #1
|
|||
|
|||
|
La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente.
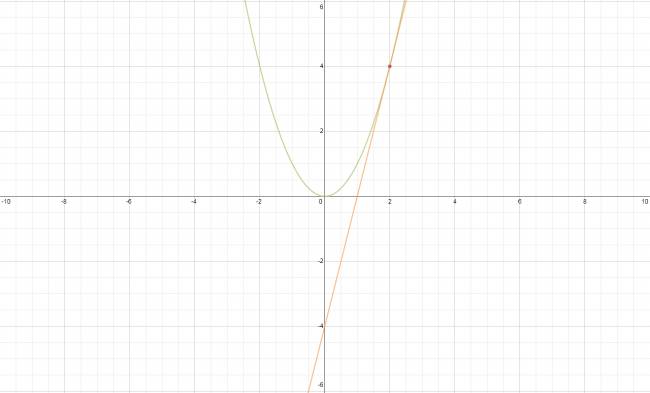
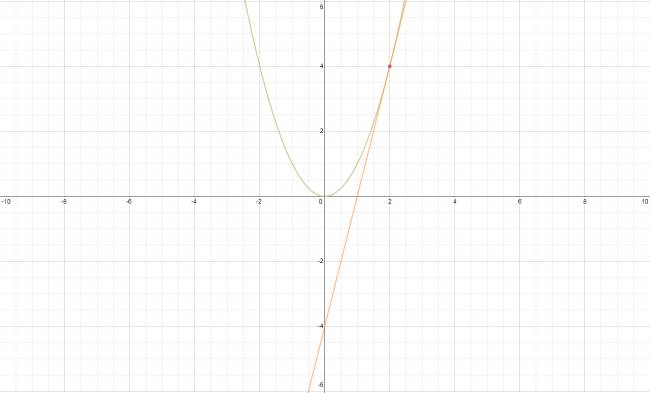
 En palabras más simples, la podríamos definir como la pendiente de la recta tangente en un punto dado la función. Explicación: Supón que te dan la función \( f(x) = x^2 \) y te piden halles la ecuación de la recta que corta a la función \( f(x) \) en el punto abscisa \( x = 2 \). Este problema se puede resolver con la derivada de la función \( f(x) \). Un ejemplo para ilustrar: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
15-08-2013, 7:23 PM
Post: #2
|
|||
|
|||
|
Derivada de una función en un punto de esta:
Este tipo de derivada permite conocer el valor de la pendiente en un punto de la función. Fórmula: $$ f'(a) = \lim_{x \to a} \frac {f(x) - f(a)}{x-a} $$ Condiciones de existencia de la derivada: Como hemos visto, la derivada se calcula por medio de límites, por lo cual, la condición necesaria para que exista la derivada de una función en un punto, es que los límites laterales existan y sean iguales en dicho punto. Referencias: · \( a \) es la abscisa del punto en que se desea calcular la pendiente de la función. · \( f(x) \) es la función de la que se desea calcular la derivada en un punto de ella. · \( f'(a) \) es la pendiente, derivada de la función en el punto \( a \) de ella. Cita Atención: como la derivada de una función en un punto de ella se calcula mediante límite, existirá únicamente si existe dicho límite. En simples palabras: si no existe el límite, no existe la derivada; si existe el límite, entonces existe la derivada. A tener en cuenta: · La derivada de una función en un punto de ella, es un número. Ecuación de la recta tangente al gráfico La ecuación de la recta tangente a \( f(x) \) por el punto \( P(a,f(a)) \) es: $$ y - f(a) = f'(a)·(x-a) $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-08-2013, 11:39 PM
Post: #3
|
|||
|
|||
|
Función derivada
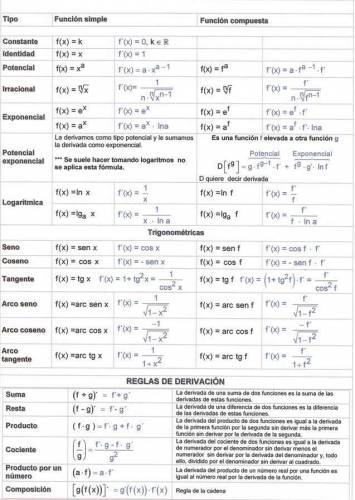
Definición: Fórmula: $$ f'(x) = \lim_{h \to 0} \frac {f(x+h) - f(x)}{h} $$ Propiedades: · Suma de derivadas: $$ y = f(x) + g(x) ⇔ y' = f'(x) + g'(x) $$ · Resta de derivadas: $$ y = f(x) - g(x) ⇔ y' = f'(x) - g'(x) $$ · Producto de derivadas: $$ y = f(x)·g(x) ⇔ y' = f'(x)·g(x) + f(x)·g'(x) $$ · Cociente de derivadas: $$ y = \frac {f(x)}{g(x)} ⇔ y' = \frac {f'(x)·g(x)-f(x)·g'(x)}{g^2(x)} $$ Tabla de derivadas: Cita Aclaraciones: · En todos los casos anteriores, \( (a,b,c) \) son números reales cualesquiera: (\( (a,b,c)∈ℝ \)). A tener en cuenta: · La derivada de una función es otra función. Derivada parcial: Cuando se tiene una expresión matemática con más de una variable, se debe utilizar este concepto. La derivada parcial de una expresión matemática con respecto a una de las variables, es la derivada de la función, tomando a las otras variables como constantes (números reales). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-09-2013, 8:19 PM
Post: #4
|
|||
|
|||
|
Teoremas relativos a las derivadas:
· Teorema de Rolle: Es un teorema matemático, relativo a las derivadas que fue enunciado y demostrado por el francés Michael Rolle (1652-1719). Enunciado: Si una función es continua en un intervalo \( [a,b] \), derivable en el intervalo \( (a,b) \) y \( f(a)=f(b) \), entonces existe al menos un punto \( c \) entre \( a \) y \( b \) para el cual \( f'( c )=0 \). · Teorema de Lagrange (del valor intermedio): Es un teorema matemático, relativo a las derivadas que fue enunciado y demostrado por el francés Joseph Louis Lagrange (1736-1813). Enunciado: Si una función es continua en el intervalo \( [a,b] \) y derivable en todo punto del intervalo \( (a,b) \), entonces existe al menos un punto \( c \) donde \( f'( c ) = \frac {f(b) - f(a)}{b - a} \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
02-10-2013, 10:00 PM
Post: #5
|
|||
|
|||
|
Relación entre el crecimiento/decrecimiento de una función y su derivada
Función creciente: Definición: Una función es creciente, si para dos valores distintos de abscisa \( x_{1} \) y \( x_{2} \) tal que \( x_{1} < x_{2} \), se cumple la siguiente relación: \( f(x_{1}) < f(x_{2}) \). Con respecto a la derivada: Una función es creciente si \( f'(x) > 0 \). Con respecto a la derivada en un punto: Una función es creciente en \( x = a \) si \( f'(a) > 0 \). Función decreciente: Una función es decreciente, si para dos valores distintos de abscisa \( x_{1} \) y \( x_{2} \) tal que \( x_{1} < x_{2} \), se cumple la siguiente relación: \( f(x_{1}) > f(x_{2}) \). Con respecto a la derivada: Una función es creciente si \( f'(x) < 0 \). Con respecto a la derivada en un punto: Una función es decreciente en \( x = a \) si \( f'(a) < 0 \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
02-11-2013, 3:29 AM
Post: #6
|
|||
|
|||
|
Relación entre el extremos absolutos (máximos y mínimos) de una función y su derivada
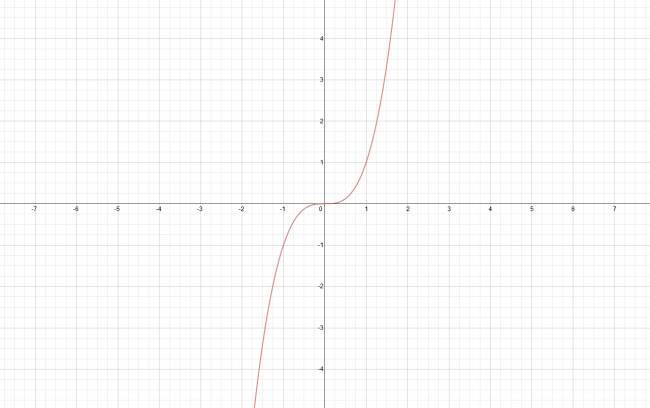
Teorema: La condición necesaria y suficiente para que una función presente un máximo o un mínimo en un punto \( x = a \), es que \( f'(a) = 0 \). Atención: No podemos afirmar que en todo punto del gráfico donde su derivada sea nula, exista un extremo absoluto; para esto veamos el siguiente ejemplo: Sea la función: \( f(x) = x^3 \), sabemos que: \( f'(0) = 0 \). Ahora bien, grafiquemos la función: Como vemos, no presenta ningún máximo ni mínimo en \( x = 0 \). O sea, siempre que haya un extremo absoluto, su derivada será nula en ese punto, pero no para todo punto del gráfico en que su derivada sea nula se podrá afirmar que presenta un extremo absoluto. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |