|
| Foro Departamento de Matemática Teóricos Geometría analítica en el plano: las secciones cónicas |
| Geometría analítica en el plano: las secciones cónicas |
|
18-10-2013, 5:11 PM
Post: #1
|
|||
|
|||
|
Las secciones cónicas
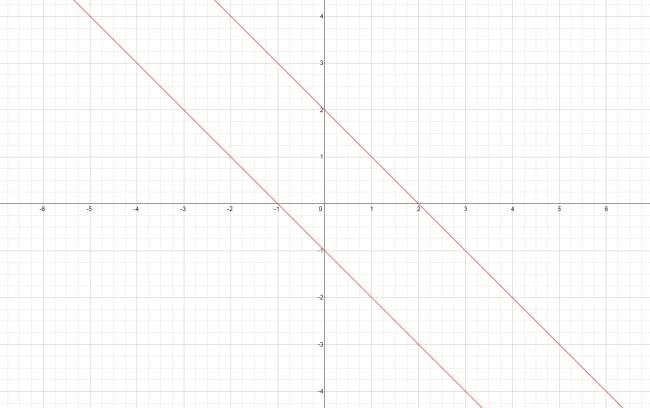
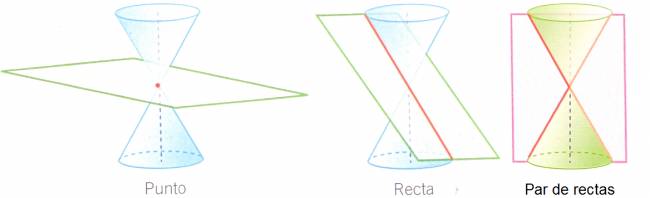
 Geométricamente podemos decir que las secciones cónicas son cuatro: circunferencia, parábola, elipse e hipérbola y resultan de la intersección de un cono con un plano. Pero visto desde un punto de vista analítico, las secciones cónicas son todas las figuras que tienen como ecuación: $$ A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 $$ Donde todos los coeficientes son reales y que cumplen la condición de que \( A, B, C \) no son simultáneamente cero. Sin embargo, no todas las figuras que presentan una ecuación como la de la fórmula son una circunferencia, parábola, elipse o hipérbola; es más, hay figuras, como es el caso de las rectas, que no cumplen esto. Veamos el siguiente ejemplo, consideremos dos rectas: \( ( r ) x + y + 1 = 0 \) y \( ( s ) x + y -2 = 0 \). Ahora las vamos a multiplicar: $$ (x + y + 1)·(x + y -2) = 0 $$ Se trata de un producto de rectas (producto de ecuaciones de las rectas) por lo que si graficamos, veríamos algo como esto: Si realizamos la correspondiente distributiva, llegaremos a la siguiente expresión: $$ x^2 + 2·x·y + y^2 - x - y - 2 = 0 $$ Sin embargo, esta ecuación corresponde a la definición de cónica de Descartes pero no lo es, por esta razón, se decidió llamarlas de otra manera y distinguir entre las cónicas tradicionales y éstas. A este tipo de expresiones que se ajustan a la definición analítica pero no a la geométrica, se les conoce como cónicas degeneradas. Hallar las rectas que conforman a la cónica degenerada (producto de rectas) Reglas: 1. Se ordenada en \( x^2 \). 2. Se aplica Bháskara. 3. Se escribe el producto de rectas. · Ver ejemplos. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
18-10-2013, 5:41 PM
Post: #2
|
|||
|
|||
|
Conociendo ecuación, reconocer si una cónica es degenerada o no
Para saber si una cónica es tradicional: cfa, parábola, elipse o hipérbola; o degenerada: producto de rectas, se debe seguir el siguiente procedimiento. 1. Estudio del género de la cónica: · Si \( A = C \) y \( B = 0 \) la cónica es una cfa. · Si \( B^2-4·A·C = 0 \) la cónica presenta género parabólico (parábola o producto de rectas paralelas). · Si \( B^2-4·A·C < 0 \) la cónica presenta género elíptico (elipse o producto de rectas secantes). · Si \( B^2-4·A·C > 0 \) la cónica presenta género hiperbólico (hipérbola o producto de rectas imaginarias: rectas con coeficientes complejos imaginarios; punto). 2. Degeneramiento de la cónica: Se debe calcular el determinante de la siguiente matriz: $$ \begin{bmatrix}{2A}&{B}&{D}\\{B}&{2C}&{E}\\{D}&{E}&{2F}\end{bmatrix} $$ Afirmaremos que la cónica es degenerada si y sólo si el resultado de dicho determinante es cero. Hallar las rectas que conforman a la cónica degenerada (producto de rectas) Reglas: 1. Se ordenada en \( x^2 \). 2. Se aplica Bháskara. 3. Se escribe el producto de rectas. · Ver ejemplos. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |