|
   |
| Foro Departamento de Matemática Problemas resueltos Escribir cónica degenerada como producto de rectas |
| Escribir cónica degenerada como producto de rectas |
|
20-10-2013, 8:14 PM
Post: #1
|
|||
|
|||
|
Conociendo la ecuación de la siguientes cónicas degeneradas, escribirlas como producto de rectas:
a. $$ x^2 + 2·x·y + y^2 - 3·x - 3·y + 2 = 0 $$ b. $$4·x^2 - 4·x·y + y^2 + 8·x - 4·y - 5 = 0 $$ |
|||
 |
|
20-10-2013, 8:17 PM
Post: #2
|
|||
|
|||
|
a.
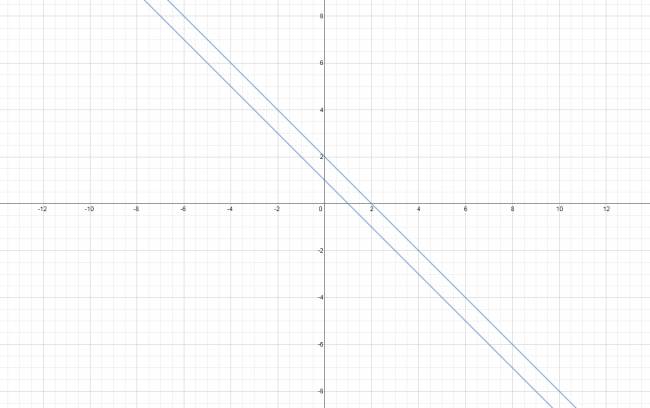
Se ordenada en \( x^2 \), resultando: $$ x^2 + (2·y-3)·x + (y^2 - 3·y + 2) = 0 $$ Luego, se resuelve por Bháskara: $$ x = \frac {-2·y + 3 ± \sqrt {(2·y-3)^2 - 4·(y^2 -3·y+2)}}{2} $$ $$ x = \frac {-2·y + 3 ± 1}{2} $$ Las rectas buscadas son: \( ( r ) y = -x +2 \) \( ( s ) y = -x +1 \) La cónica degenerada se puede escribir como: $$ (x+y-2)·(x+y-1)=0 $$ Acá va su representación gráfica:  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
 |
|
20-10-2013, 8:30 PM
Post: #3
|
|||
|
|||
|
b.
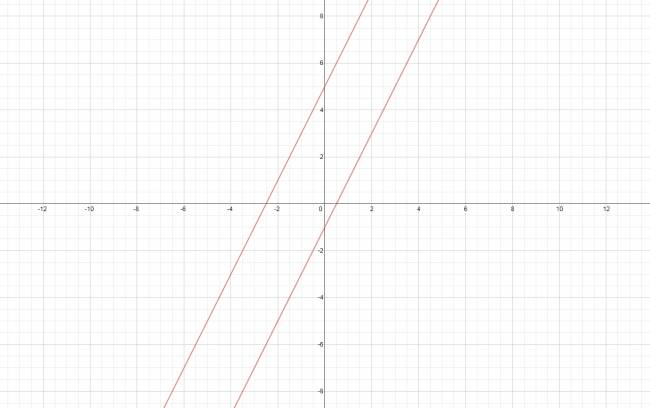
Procedemos análogamente que en el caso anterior, ordenando en \( x^2 \): $$ 4·x^2 + (-4·y+8)·x + (y^2-4·y-5)=0 $$ Aplicamos Bháskara: $$ x = \frac {4·y - 8 ± \sqrt {(-4·y + 8)^2 - 4^2·(y^2-4·y-5)}}{2·4} $$ $$ x = \frac {4·y - 8 ± 12}{8} $$ Las rectas buscadas son: \( ( r ) 2·x - y - 1 = 0 \) \( ( s ) 2·x - y + 5 = 0 \) La cónica degenerada puede escribirse como: $$ (2·x - y - 1)·(2·x - y +5) = 0 $$ Acá va su representación gráfica:  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |