18-10-2013, 5:11 PM
Las secciones cónicas

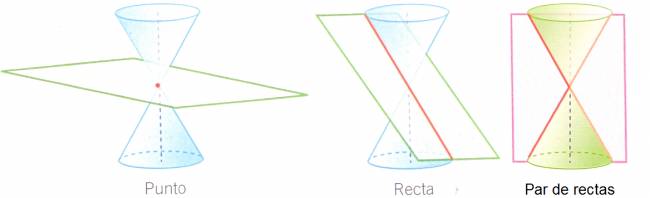
Geométricamente podemos decir que las secciones cónicas son cuatro: circunferencia, parábola, elipse e hipérbola y resultan de la intersección de un cono con un plano.
Pero visto desde un punto de vista analítico, las secciones cónicas son todas las figuras que tienen como ecuación:
$$ A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 $$
Donde todos los coeficientes son reales y que cumplen la condición de que \( A, B, C \) no son simultáneamente cero.
Sin embargo, no todas las figuras que presentan una ecuación como la de la fórmula son una circunferencia, parábola, elipse o hipérbola; es más, hay figuras, como es el caso de las rectas, que no cumplen esto.
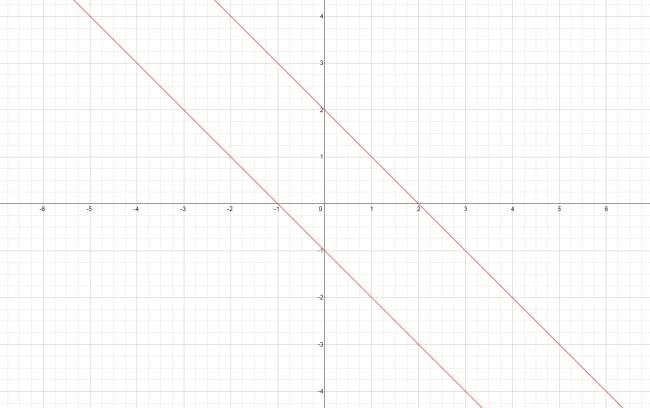
Veamos el siguiente ejemplo, consideremos dos rectas: \( ( r ) x + y + 1 = 0 \) y \( ( s ) x + y -2 = 0 \). Ahora las vamos a multiplicar:
$$ (x + y + 1)·(x + y -2) = 0 $$
Se trata de un producto de rectas (producto de ecuaciones de las rectas) por lo que si graficamos, veríamos algo como esto:
Si realizamos la correspondiente distributiva, llegaremos a la siguiente expresión:
$$ x^2 + 2·x·y + y^2 - x - y - 2 = 0 $$
Sin embargo, esta ecuación corresponde a la definición de cónica de Descartes pero no lo es, por esta razón, se decidió llamarlas de otra manera y distinguir entre las cónicas tradicionales y éstas. A este tipo de expresiones que se ajustan a la definición analítica pero no a la geométrica, se les conoce como cónicas degeneradas.
Hallar las rectas que conforman a la cónica degenerada (producto de rectas)
Reglas:
1. Se ordenada en \( x^2 \).
2. Se aplica Bháskara.
3. Se escribe el producto de rectas.
· Ver ejemplos.

Geométricamente podemos decir que las secciones cónicas son cuatro: circunferencia, parábola, elipse e hipérbola y resultan de la intersección de un cono con un plano.
Pero visto desde un punto de vista analítico, las secciones cónicas son todas las figuras que tienen como ecuación:
$$ A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 $$
Donde todos los coeficientes son reales y que cumplen la condición de que \( A, B, C \) no son simultáneamente cero.
Sin embargo, no todas las figuras que presentan una ecuación como la de la fórmula son una circunferencia, parábola, elipse o hipérbola; es más, hay figuras, como es el caso de las rectas, que no cumplen esto.
Veamos el siguiente ejemplo, consideremos dos rectas: \( ( r ) x + y + 1 = 0 \) y \( ( s ) x + y -2 = 0 \). Ahora las vamos a multiplicar:
$$ (x + y + 1)·(x + y -2) = 0 $$
Se trata de un producto de rectas (producto de ecuaciones de las rectas) por lo que si graficamos, veríamos algo como esto:
Si realizamos la correspondiente distributiva, llegaremos a la siguiente expresión:
$$ x^2 + 2·x·y + y^2 - x - y - 2 = 0 $$
Sin embargo, esta ecuación corresponde a la definición de cónica de Descartes pero no lo es, por esta razón, se decidió llamarlas de otra manera y distinguir entre las cónicas tradicionales y éstas. A este tipo de expresiones que se ajustan a la definición analítica pero no a la geométrica, se les conoce como cónicas degeneradas.
Hallar las rectas que conforman a la cónica degenerada (producto de rectas)
Reglas:
1. Se ordenada en \( x^2 \).
2. Se aplica Bháskara.
3. Se escribe el producto de rectas.
· Ver ejemplos.