|
| Foro Departamento de Matemática Teóricos Función racional |
| Función racional |
|
24-01-2013, 5:12 PM
Post: #1
|
|||
|
|||
|
Función racional
Definición: Una función racional, es una función que resulta del cociente de dos funciones polinómicas particulares. Dicho de una forma más simple, toda función racional es de la forma: $$ f(x) = \frac {p(x)}{q(x)} $$ Por definición de división, el polinomio \( q(x) \) no puede ser nulo. Además para que estemos en presencia de una función racional, la función polinómica \( p(x) \) no puede ser divisible entre \( q(x) \). También, para que estemos en presencia de una función racional y no una polinómica, la función \( q(x) \) debe presentar al menos una variable. Raíces de la función racional: Las raíces de esta función, son las raíces del polinomio dividendo (aquel que se encuentra en el numerador de la fracción), siempre y cuando no sean las mismas que presenta el polinomio divisor (aquel que se encuentra en el denominador de al fracción). Todas las raíces que presenten el polinomio numerador y el denominador a la vez, serán tomadas como asíntotas y no raíces. Dominio de una función racional: Por definición de división, el divisor nunca puede ser cero, por esta razón las raíces del polinomio divisor (en nuestro caso \( q(x) \)) deben ser extraídas del dominio de la función. Si nuestro polinomio divisor \( q(x) \), presenta las raíces \( \alpha_{1}, \alpha_{2}, \alpha_{3}, ... \), el dominio de la función será: $$ D = ℝ - \left\{ \alpha_{1}, \alpha_{2}, \alpha_{3}, ... \right\} $$ Asíntotas de una función racional: Una función racional puede presentar los tres tipos de asíntotas existentes: horizontales, verticales, y oblicuas. · Verticales: Habrá una asíntota vertical en cada valor que fue extraído del dominio. · Aprender a calcular las asíntotas. Representación gráfica de una función racional: La representación gráfica de una función racional recibe el nombre de hipérbola equilátera. Caso particular: Todas las funciones racionales de la forma: $$ f(x) = \frac {a·x+b}{c·x + d}, ∀(a,b,c,d)∈ℝ $$ Son consideradas un caso particular de las funciones racionales. Se han estudiado con mayor profundidad debido a lo común que son. Condición de existencia: Estas funciones son racionales, siempre y cuando cumplan la condición de que: \( a·d≠b·c \). Además que \( c \) nunca pueden ser nulo. Raíces: $$ S = \left\{ -\frac {b}{a} \right\} $$ Dominio: $$ D = \left\{ -\frac {d}{c} \right\} $$ Asíntotas: · Asíntota vertical : $$ x = -\frac {d}{c} $$ · Asíntota horizontal: $$ y = \frac {a}{c} $$ Este caso particular de función racional no presenta asíntotas oblicuas. Ordenada en el origen: $$ P \left [ 0, \frac {b}{c} \right ] $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
01-09-2013, 8:49 AM
Post: #2
|
|||
|
|||
|
Ejemplo:
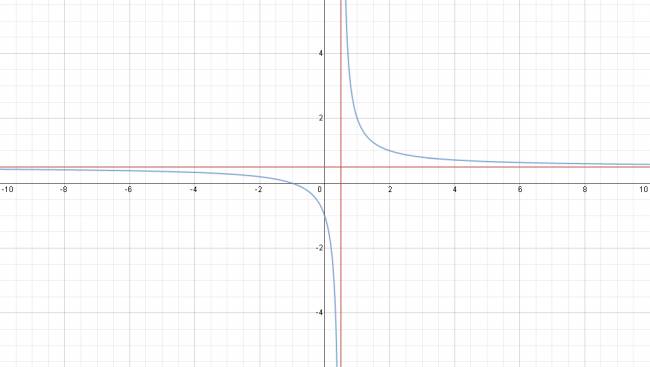
Código Sea la función \( f:ℝ→ℝ \): $$ f(x) = \frac {2·x+2}{4·x-2} $$ Estudiar: raíces, dominio, asíntotas, ordenada en el origen, y realizar bosquejo de gráfico. · Raíces: Igualo el numerador a 0, resultando de la siguiente manera: $$ 2·x+2=0 ⇒ 2·x = -2 ⇒ x = -1 $$ $$ S = \left\{ -1 \right\} $$ · Dominio: Igualo el denominador a 0, resultando de la siguiente manera: $$ 4·x-2=0 ⇒ 4·x = 2 ⇒ x = \frac {1}{2} $$ $$ D = ℝ - \left\{ \frac {1}{2} \right\} $$ · Ordenada en el origen: Calculo haciendo el valor numérico \( f(0) \): $$ f(x) = \frac {2·x+2}{4·x-2} ⇒ f(0) = \frac {2·0+2}{4·0-2} = -1 $$ Gráfico de la función con sus asíntotas: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |