24-01-2013, 5:12 PM
Función racional
Definición:
Una función racional, es una función que resulta del cociente de dos funciones polinómicas particulares.
Dicho de una forma más simple, toda función racional es de la forma:
$$ f(x) = \frac {p(x)}{q(x)} $$
Por definición de división, el polinomio \( q(x) \) no puede ser nulo. Además para que estemos en presencia de una función racional, la función polinómica \( p(x) \) no puede ser divisible entre \( q(x) \). También, para que estemos en presencia de una función racional y no una polinómica, la función \( q(x) \) debe presentar al menos una variable.
Raíces de la función racional:
Las raíces de esta función, son las raíces del polinomio dividendo (aquel que se encuentra en el numerador de la fracción), siempre y cuando no sean las mismas que presenta el polinomio divisor (aquel que se encuentra en el denominador de al fracción). Todas las raíces que presenten el polinomio numerador y el denominador a la vez, serán tomadas como asíntotas y no raíces.
Dominio de una función racional:
Por definición de división, el divisor nunca puede ser cero, por esta razón las raíces del polinomio divisor (en nuestro caso \( q(x) \)) deben ser extraídas del dominio de la función.
Si nuestro polinomio divisor \( q(x) \), presenta las raíces \( \alpha_{1}, \alpha_{2}, \alpha_{3}, ... \), el dominio de la función será:
$$ D = ℝ - \left\{ \alpha_{1}, \alpha_{2}, \alpha_{3}, ... \right\} $$
Asíntotas de una función racional:
Una función racional puede presentar los tres tipos de asíntotas existentes: horizontales, verticales, y oblicuas.
· Verticales:
Habrá una asíntota vertical en cada valor que fue extraído del dominio.
· Aprender a calcular las asíntotas.
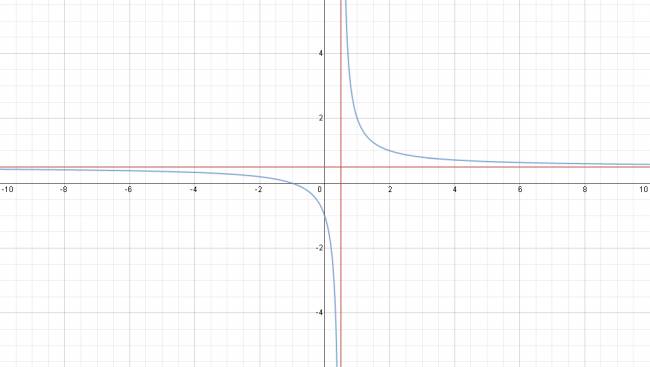
Representación gráfica de una función racional:
La representación gráfica de una función racional recibe el nombre de hipérbola equilátera.
Caso particular:
Todas las funciones racionales de la forma:
$$ f(x) = \frac {a·x+b}{c·x + d}, ∀(a,b,c,d)∈ℝ $$
Son consideradas un caso particular de las funciones racionales. Se han estudiado con mayor profundidad debido a lo común que son.
Condición de existencia:
Estas funciones son racionales, siempre y cuando cumplan la condición de que: \( a·d≠b·c \). Además que \( c \) nunca pueden ser nulo.
Raíces:
$$ S = \left\{ -\frac {b}{a} \right\} $$
Dominio:
$$ D = \left\{ -\frac {d}{c} \right\} $$
Asíntotas:
· Asíntota vertical :
$$ x = -\frac {d}{c} $$
· Asíntota horizontal:
$$ y = \frac {a}{c} $$
Este caso particular de función racional no presenta asíntotas oblicuas.
Ordenada en el origen:
$$ P \left [ 0, \frac {b}{c} \right ] $$
Definición:
Una función racional, es una función que resulta del cociente de dos funciones polinómicas particulares.
Dicho de una forma más simple, toda función racional es de la forma:
$$ f(x) = \frac {p(x)}{q(x)} $$
Por definición de división, el polinomio \( q(x) \) no puede ser nulo. Además para que estemos en presencia de una función racional, la función polinómica \( p(x) \) no puede ser divisible entre \( q(x) \). También, para que estemos en presencia de una función racional y no una polinómica, la función \( q(x) \) debe presentar al menos una variable.
Raíces de la función racional:
Las raíces de esta función, son las raíces del polinomio dividendo (aquel que se encuentra en el numerador de la fracción), siempre y cuando no sean las mismas que presenta el polinomio divisor (aquel que se encuentra en el denominador de al fracción). Todas las raíces que presenten el polinomio numerador y el denominador a la vez, serán tomadas como asíntotas y no raíces.
Dominio de una función racional:
Por definición de división, el divisor nunca puede ser cero, por esta razón las raíces del polinomio divisor (en nuestro caso \( q(x) \)) deben ser extraídas del dominio de la función.
Si nuestro polinomio divisor \( q(x) \), presenta las raíces \( \alpha_{1}, \alpha_{2}, \alpha_{3}, ... \), el dominio de la función será:
$$ D = ℝ - \left\{ \alpha_{1}, \alpha_{2}, \alpha_{3}, ... \right\} $$
Asíntotas de una función racional:
Una función racional puede presentar los tres tipos de asíntotas existentes: horizontales, verticales, y oblicuas.
· Verticales:
Habrá una asíntota vertical en cada valor que fue extraído del dominio.
· Aprender a calcular las asíntotas.
Representación gráfica de una función racional:
La representación gráfica de una función racional recibe el nombre de hipérbola equilátera.
Caso particular:
Todas las funciones racionales de la forma:
$$ f(x) = \frac {a·x+b}{c·x + d}, ∀(a,b,c,d)∈ℝ $$
Son consideradas un caso particular de las funciones racionales. Se han estudiado con mayor profundidad debido a lo común que son.
Condición de existencia:
Estas funciones son racionales, siempre y cuando cumplan la condición de que: \( a·d≠b·c \). Además que \( c \) nunca pueden ser nulo.
El problema radica en que si se cumple la igualdad \( a·d ≠ b·c \) es porque son ecuaciones equivalentes, o sea, que tienen el mismo conjunto solución.
Ejemplo:
La siguiente función cumple que la anterior igualdad:
$$ f(x) = \frac {3·x + 9}{2·x + 6} $$
Pero si prestamos atención, podemos quitar de factor común:
$$ f(x) = \frac {3·(x + 3)}{2·(x + 3)} $$
Como vemos, el factor \( x + 3 \) se repite tanto en el numerador como en el denominador, po lo que podemos cancelarlo, resultando en:
$$ f(x) = \frac {3}{2} $$
Esta función es equivalente a la primera, y como sabemos, esta función es constante.
Toda función racional debe cumplir que \( a·d ≠ b·c \), porque si esto sucede, el polinomio del denominador es equivalente al del denominador.
Demostración:
Hipótesis:
· La ecuación del numerador es equivalente a la del denominador.
\( \frac {a·x + b}{c·x + d} \)
Tesis:
\( a·d = b·c \)
Demostración:
\( \frac {a·x + b}{c·x + d} \)
Despejamos \( x \) del numerador, resultando en: \( x = \frac {-b}{a} \).
Despejamos \( x \) del denominador, resultando en: \( x = \frac {-d}{c} \).
Por hipótesis sabemos que ambos valores de \( x \) son iguales, por lo que podemos igualarlos.
$$ \frac {-b}{a} = \frac {-d}{c} ⇒ -a·d = -b·c ⇒ a·d = b·c $$
Ejemplo:
La siguiente función cumple que la anterior igualdad:
$$ f(x) = \frac {3·x + 9}{2·x + 6} $$
Pero si prestamos atención, podemos quitar de factor común:
$$ f(x) = \frac {3·(x + 3)}{2·(x + 3)} $$
Como vemos, el factor \( x + 3 \) se repite tanto en el numerador como en el denominador, po lo que podemos cancelarlo, resultando en:
$$ f(x) = \frac {3}{2} $$
Esta función es equivalente a la primera, y como sabemos, esta función es constante.
Toda función racional debe cumplir que \( a·d ≠ b·c \), porque si esto sucede, el polinomio del denominador es equivalente al del denominador.
Demostración:
Hipótesis:
· La ecuación del numerador es equivalente a la del denominador.
\( \frac {a·x + b}{c·x + d} \)
Tesis:
\( a·d = b·c \)
Demostración:
\( \frac {a·x + b}{c·x + d} \)
Despejamos \( x \) del numerador, resultando en: \( x = \frac {-b}{a} \).
Despejamos \( x \) del denominador, resultando en: \( x = \frac {-d}{c} \).
Por hipótesis sabemos que ambos valores de \( x \) son iguales, por lo que podemos igualarlos.
$$ \frac {-b}{a} = \frac {-d}{c} ⇒ -a·d = -b·c ⇒ a·d = b·c $$
Raíces:
$$ S = \left\{ -\frac {b}{a} \right\} $$
Dominio:
$$ D = \left\{ -\frac {d}{c} \right\} $$
Asíntotas:
· Asíntota vertical :
$$ x = -\frac {d}{c} $$
· Asíntota horizontal:
$$ y = \frac {a}{c} $$
Este caso particular de función racional no presenta asíntotas oblicuas.
Ordenada en el origen:
$$ P \left [ 0, \frac {b}{c} \right ] $$