|
| Foro Departamento de Matemática Problemas resueltos Calcular los siguientes límites con radicales |
| Calcular los siguientes límites con radicales |
|
13-08-2013, 7:37 PM
Post: #1
|
|||
|
|||
|
1.
$$ \lim_{x \to +∞} \frac {\sqrt {x}}{\sqrt {x+\sqrt {x}}} $$ 2. $$ \lim_{x \to +∞} \frac {\sqrt {4·x^2-3·x}}{x} $$ 3. $$ \lim_{x \to +∞} \frac {x}{\sqrt [4]{x^3}} $$ 4. $$ \lim_{x \to 1^{+}} \frac {x·\sqrt {x^2-1}}{x^2-x} $$ 5. $$ \lim_{x \to 4^{-}} \frac {x-4}{\sqrt{(x-4)^2}} $$ |
|||
|
13-08-2013, 7:41 PM
Post: #2
|
|||
|
|||
|
Cita $$ \lim_{x \to +∞} \frac {\sqrt {x}}{\sqrt {x+\sqrt {x}}} $$ $$ \lim_{x \to +∞} \frac {\sqrt {x}}{\sqrt {x+\sqrt {x}}} = \lim_{x \to +∞} \frac {\sqrt {x}}{\sqrt {x}} = 1 $$ Podemos afirmar que \( \sqrt {x} \) y \( \sqrt {x+\sqrt {x}} \) son infinitésimos equivalentes cuando \( x \to +∞ \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-08-2013, 7:41 PM
Post: #3
|
|||
|
|||
|
Cita $$ \lim_{x \to +∞} \frac {\sqrt {4·x^2-3·x}}{x} $$ $$ \lim_{x \to +∞} \frac {\sqrt {4·x^2-3·x}}{x} = \lim_{x \to +∞} \frac {2·x}{x} = 2 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-08-2013, 7:41 PM
Post: #4
|
|||
|
|||
|
Cita $$ \lim_{x \to +∞} \frac {x}{\sqrt [4]{x^3}} $$ $$ \lim_{x \to +∞} \frac {x}{\sqrt [4]{x^3}} = \lim_{x \to +∞} \sqrt [4]{x} = +∞ $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-08-2013, 7:42 PM
Post: #5
|
|||
|
|||
|
Cita $$ \lim_{x \to 1^{+}} \frac {x·\sqrt {x^2-1}}{x^2-x} $$ 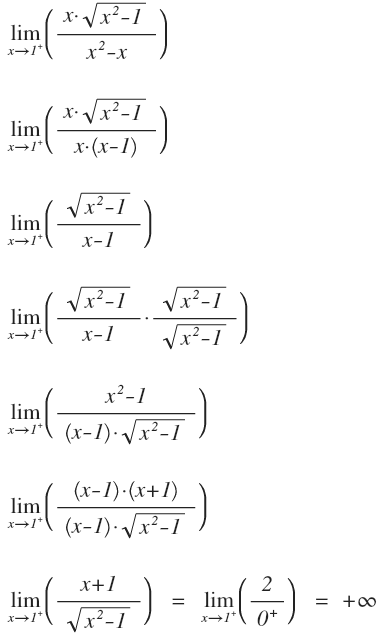 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-08-2013, 7:50 PM
Post: #6
|
|||
|
|||
|
Cita $$ \lim_{x \to 4^{-}} \frac {x-4}{\sqrt{(x-4)^2}} $$ $$ \lim_{x \to 4^{-}} \frac {x-4}{\sqrt{(x-4)^2}} = \lim_{x \to 4^{-}} \frac {x-4}{|x-4|} = -1 $$ Esto es cierto, ya que si nos acercamos a 4 por la izquierda en la función \( f(x) = x-4 \), a este le corresponden valores negativos. La función que estudiamos que estamos estudiando, va a tener un comportamiento parecido a la anterior, por esta razón lo podemos deducir. En efecto: $$ g(x) = \frac {x-4}{\sqrt{(x-4)^2}} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |