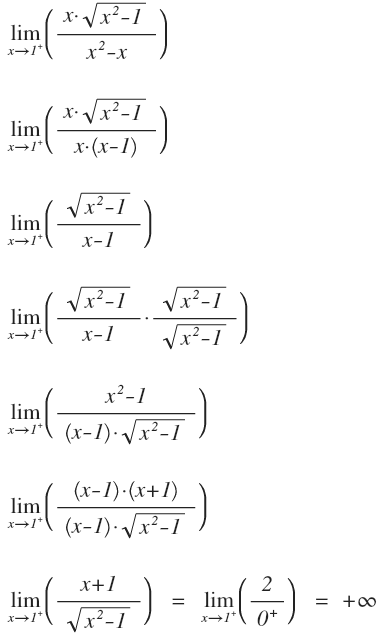13-08-2013, 7:37 PM
1.
$$ \lim_{x \to +∞} \frac {\sqrt {x}}{\sqrt {x+\sqrt {x}}} $$
2.
$$ \lim_{x \to +∞} \frac {\sqrt {4·x^2-3·x}}{x} $$
3.
$$ \lim_{x \to +∞} \frac {x}{\sqrt [4]{x^3}} $$
4.
$$ \lim_{x \to 1^{+}} \frac {x·\sqrt {x^2-1}}{x^2-x} $$
5.
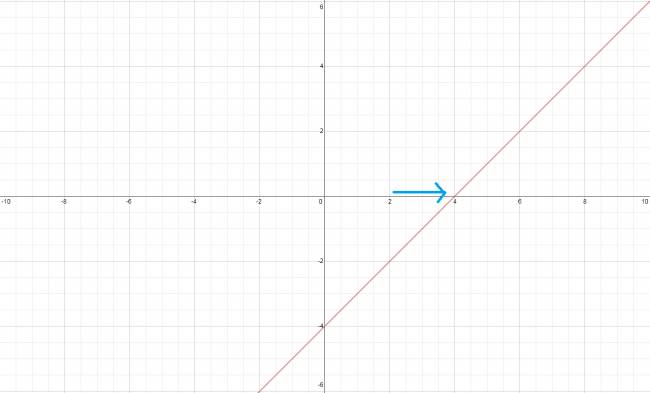
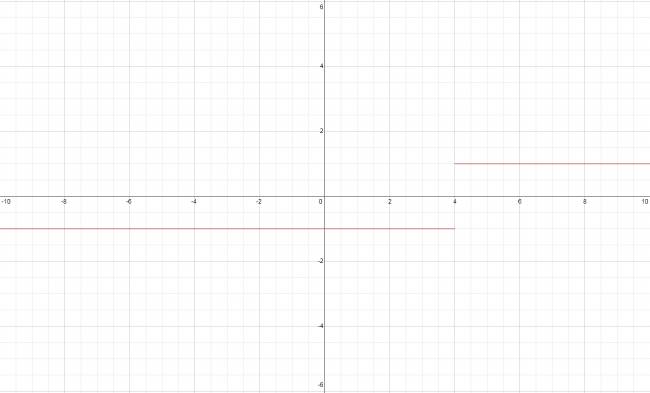
$$ \lim_{x \to 4^{-}} \frac {x-4}{\sqrt{(x-4)^2}} $$
$$ \lim_{x \to +∞} \frac {\sqrt {x}}{\sqrt {x+\sqrt {x}}} $$
2.
$$ \lim_{x \to +∞} \frac {\sqrt {4·x^2-3·x}}{x} $$
3.
$$ \lim_{x \to +∞} \frac {x}{\sqrt [4]{x^3}} $$
4.
$$ \lim_{x \to 1^{+}} \frac {x·\sqrt {x^2-1}}{x^2-x} $$
5.
$$ \lim_{x \to 4^{-}} \frac {x-4}{\sqrt{(x-4)^2}} $$