|
| Foro Departamento de Matemática Problemas resueltos Problemas de familia de rectas |
| Problemas de familia de rectas |
|
16-05-2013, 1:44 AM
Post: #1
|
|||
|
|||
|
1. Analizar si las siguientes dos familias forman haz o no:
$$ (t) (k+1)·x + (2·k+2)·y - 5·k + 3 = 0 $$ $$ (s) (2·q+1)·x + (-q+3)·y + q - 10 = 0 $$ 2. \( (t) (2·k+1)·x + (k-3)·y - k + 5 = 0 \) a. Hallar la recta de la familia que pasa por \( A (-1, 2) \). b. Hallar la recta que sea paralela a \( 9·x + y - 7 = 0 \). c. Hallar la recta que sea perpendicular a \( x + 5·y + 6 = 0 \). d. Hallar la recta que sea paralela a \( O \vec x \). e. Hallar la recta que sea paralela a \( O \vec y \). f. Investigar familia. 3. Sea la familia de rectas: \( 2·k·x + (k^2-1)·y + 2·k^2 - 2·k + 4 = 0 \), hallar la región del plano por donde pasan dos rectas de la familia, una o ninguna. |
|||
|
16-05-2013, 1:51 AM
Post: #2
|
|||
|
|||
|
Cita (marcos364) 1. Analizar si las siguientes dos familias forman haz o no: (t)(k+1)⋅x+(2⋅k+2)⋅y−5⋅k+3=0 Hallamos la pendiente de la familia. Observamos y vemos que la ecuación de la recta anterior es de la forma: \( a·x + b·y + c = 0 \), cuya pendiente se puede calcular como: \( m = - \frac {a}{b} \) En nuestro caso: $$ m = - \frac {(k+1)}{(2·k+2)} $$ Esto sucede bajo la condición de que \( k ≠ -1 \), ya que en tal caso quedaría una división entre 0, lo cual no es posible. Pero vemos que la podemos simplificar: $$ m = \frac {-1·(k+1)}{2·(k+1)} ⇒ m = - \frac {1}{2} $$ Cita Como vemos que la pendiente no depende de \( k \), entonces \( (t) \) es un haz impropio. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:02 AM
Post: #3
|
|||
|
|||
|
Cita (marcos364) (s)(2⋅q+1)⋅x+(−q+3)⋅y+q−10=0 Igual que en el caso anterior: hallamos la pendiente (m). $$ m = - \frac {-(2·q + 1)}{(-q + 3)} $$ Bajo la condición de que \( q ≠ 3 \). Como la pendiente depende de \( q \), no forman haz propio. Ahora vamos a investigar si forman haz propio o si no forman haz. Aplicamos distributiva: $$ (2·q+1)·x + (-q+3)·y + q - 10 = 0 $$ $$ 2·q·x + x -q·y + 3·y + q - 10 = 0 $$ Ordenamos en el parámetro: $$ (2·x - y + 1)·q + (x + 3·y - 10) = 0 $$ Igualamos cada coeficiente a 0 y formamos un sistema de ecuaciones: $$ \begin{cases} (2·x - y + 1) \\ (x + 3·y - 10) \end{cases} $$ Resolvemos y llegamos a: $$ \left\{ 1, 3 \right\} $$ Como llegamos a un valor finito, un punto, podemos afirmar que: la familia \( s \) forma un haz propio de centro \( P (1, 3) \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:15 AM
Post: #4
|
|||
|
|||
|
Cita (marcos364) 2. (t)(2⋅k+1)⋅x+(k−3)⋅y−k+5=0a. Hallar la recta de la familia que pasa por A(−1,2). $$ (t) (2·k+1)·x + (k-3)·y - k + 5 = 0 $$ Vamos a sustituir las coordenadas del punto por \( x \) e \( y \). $$ (2·k+1)·(-1) + (k-3)·(2) - k + 5 = 0 $$ $$ k = -2 $$ Una vez que hallamos el valor del parámetro lo reemplazamos en la ecuación original: $$ (2·(-2)+1)·(-1) + ((-2)-3)·(2) - (-2) + 5 = 0 $$ Respuesta: $$ -3·x + 5·y + 7 = 0 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:31 AM
Post: #5
|
|||
|
|||
|
Cita (marcos364) b. Hallar la recta que sea paralela a 9⋅x+y−7=0. Hallamos la pendiente de la recta dada: $$ m = - 9 $$ Y la pendiente de la familia de rectas: $$ m = \frac {-2·k - 1}{k - 3} $$ Con la condición de que: \( k ≠ 3 \). Igualamos las pendientes: $$ \frac {-2·k - 1}{k - 3} = -9 ⇒ -2·k - 1 = -9·(k - 3) ⇒ k = 4 $$ Sustituimos en la ecuación de la familia de rectas: $$ (2·4+1)·x + (4-3)·y - 4 + 5 = 0 $$ Respuesta: $$ 9·x + y + 1 = 0 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:44 AM
Post: #6
|
|||
|
|||
|
Cita (marcos364) c. Hallar la recta que sea perpendicular a x−5⋅y+6=0. $$ m = - \frac {1}{5} $$ Igualamos las pendientes y resolvemos: $$ \frac {-2·k - 1}{k - 3} = - \frac {1}{5} ⇒ k = 2 $$ Reemplazamos en la ecuación de la familia y obtenemos: $$ 5·x - y + 3 = 0 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:51 AM
Post: #7
|
|||
|
|||
|
Cita (marcos364) d. Hallar la recta que sea paralela a Ox⃗ . $$ (2·k+1)·x + (k-3)·y - k + 5 = 0 $$ Para que esto suceda, igualamos a cero: $$ 2·k+1 = 0 ⇒ k - \frac {1}{2} $$ Reemplazamos y resulta en: $$ y = \frac {11}{7} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:54 AM
Post: #8
|
|||
|
|||
|
Cita (marcos364) e. Hallar la recta que sea paralela a Oy⃗ . $$ (2·k+1)·x + (k-3)·y - k + 5 = 0 $$ Por lo que igualamos a cero: $$ k-3 = 0 ⇒ k = 3 $$ Reemplazamos: $$ x = - \frac {2}{7} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 2:58 AM
Post: #9
|
|||
|
|||
|
Cita (marcos364) f. Investigar familia. $$ m = \frac {-(2·k + 1)}{k - 3}, k≠3 $$ No forma haz impropio. Ordenamos en el parámetro: $$ (2·x + y - 1)·k + (x - 3·y + 5) = 0 $$ Formamos el sistema: $$ \begin{cases} 2·x + y - 1 \\ x - 3·y + 5 \end{cases} $$ \( (t) \) forma un haz propio de centro \( P (-\frac {2}{7}, \frac {11}{7}) \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
16-05-2013, 3:18 AM
Post: #10
|
|||
|
|||
|
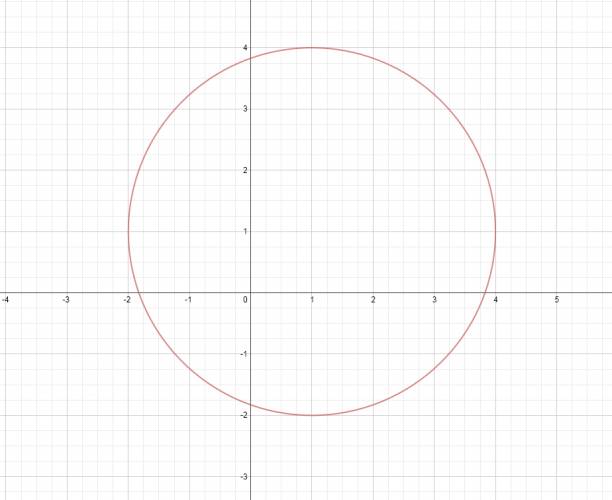
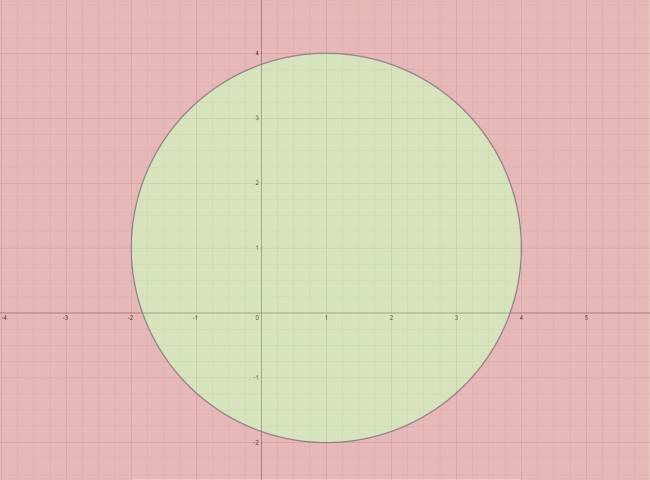
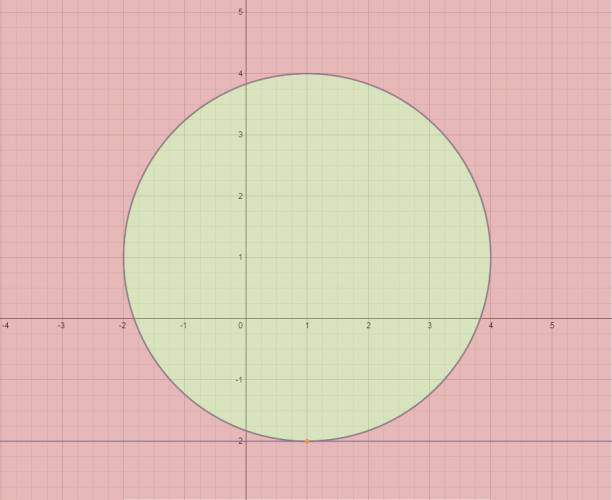
Cita (marcos364) 3. Sea la familia de rectas: 2⋅k⋅x+(k2−1)⋅y+2⋅k2−2⋅k+4=0, hallar la región del plano por donde pasan dos rectas de la familia, una o ninguna. Como el problema dice "estudiar en qué región del plano pasan dos, una o ninguna", el problema está asociado a una ecuación de segundo grado, y en particular a su discriminante. $$ \Delta = b^2 - 4·a·c $$  Se refiere a una ecuación de segundo grado en el parámetro. Ordenamos en el parámetro: $$ (y+2)·k^2 + (2·x - 2)·k + (-y+4)=0 $$ Esto se cumple siempre y cuando \( y ≠ -2 \). $$ \Delta = (2·x-2)^2 - 4·(y+2)·(-y+4) $$ $$ \Delta = 4·(x^2 + y^2 - 2·x - 2·y - 7) $$ Igualamos a cero y graficamos la cfa: $$ x^2 + y^2 - 2·x - 2·y - 7 = 0 $$ Resolvemos gráficamente: Cita Referencias: \( \Delta = 0 → \) por cada punto pasa una recta de la familia. \( \Delta > 0 → \) por cada punto pasan dos rectas de la familia. \( \Delta < 0 → \) no pasa ninguna recta de la familia. Aún nos falta evaluar el caso en que \( y = -2 \): $$ (y+2)·k^2 + (2·x - 2)·k + (-y+4)=0 $$ $$ (2·x - 2)·k + 6 = 0 $$ En el caso en que: \( x ≠ 1 → \) pasa una recta. \( x = 1 → \) no pasa ninguna recta. Por el punto \( A (1,-2) \) no pasa ninguna recta de la familia. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |