|
| Foro Departamento de Matemática Problemas resueltos Sistema de inecuaciones |
| Sistema de inecuaciones |
|
06-10-2012, 2:16 AM
Post: #1
|
|||
|
|||
|
Resuelve gráficamente el siguiente sistema de inecuaciones:
x ≤ 2 y ≤ 2·x + 1 y ≥ 2/3·x - 1 y ≤ -3·x + 8 |
|||
|
06-10-2012, 2:22 AM
Post: #2
|
|||
|
|||
|
Analizaré cada caso por particular para luego graficar el conjunto total:
x ≤ 2 → significa que en el eje horizontal (abscisa), en dos se deberá trazar una recta paralela al eje vertical (ordenada). Se quieren los valores menores o iguales que 2, por lo que se coloreará la parte izquierda. La recta también va pintada. Gráficamente es: 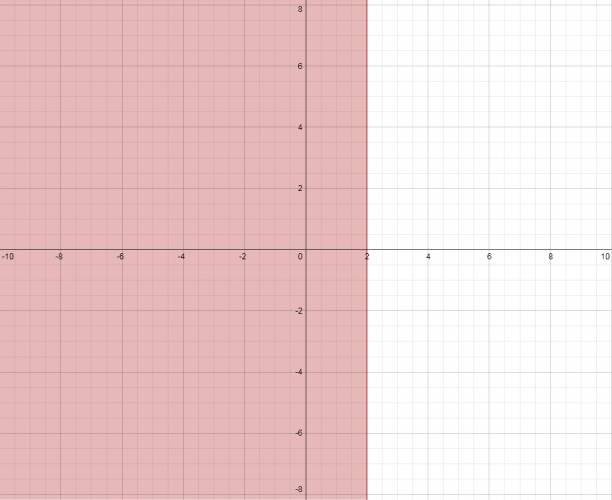 y ≤ 2·x + 1 → intentaremos dejar todos los términos en un único miembro, por ejemplo: y ≤ 2·x + 1 0 ≤ 2·x - y + 1 ⇔ 2·x - y + 1 ≥ 0 Ahora volveremos a la ecuación que tenía a la y de un lado y los demás términos del otro, me refiero a esta: y = 2·x + 1 Tomaremos unos valores (los que queramos, mínimo dos), por ejemplo: 0 y -2. Ambos números los sustituiremos por x y que haremos las cuentas, el resultado será el valor de y para su correspondiente x. La recta también va pintada. 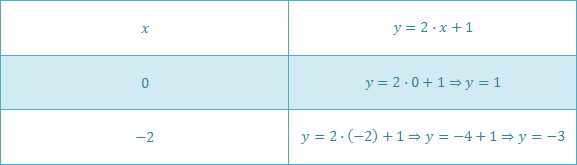 Gracias a esto hemos deducido que la recta pasa por: (0,1) y (-2,-3). Recordemos que por un punto pasan infinitas rectas, pero por dos puntos pasa una única. Graficamos ambos puntos y trazamos la recta que pasa por estos. Tomamos un punto testigo que no esté incluido en la recta, sino que esté a su derecha o a su izquierda. Yo tomaré el origen (0,0) que está a la derecha de la recta. Volveré a la inecuación que hoy despejé: 2·x - y + 1 ≥ 0 y sustituiré los valores en la anterior inecuación de la siguiente forma: 2·x - y + 1 → 2·0 - 0 + 1 = +1 Tomé un valor cualquiera que se encuentra a la derecha de la recta y me dio positivo, esto quiere decir que a la derecha de la gráfica se encuentra los valores que positivo, a la izquierda negativos y sobre la misma recta 0. Se me pidió los mayores o iguales a 0, o sea, los valores que se encuentran a la derecha de la recta, y la recta mismo. Gráficamente es: 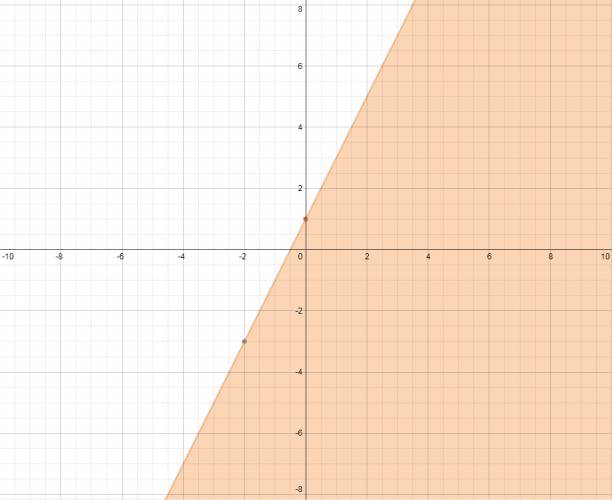 Se trabaja análogamente con las siguientes dos rectas. Es muy largo de redactar el paso a paso y como el procedimiento es igual al anterior sólo dejaré los gráficos. y ≥ 2/3·x - 1 : 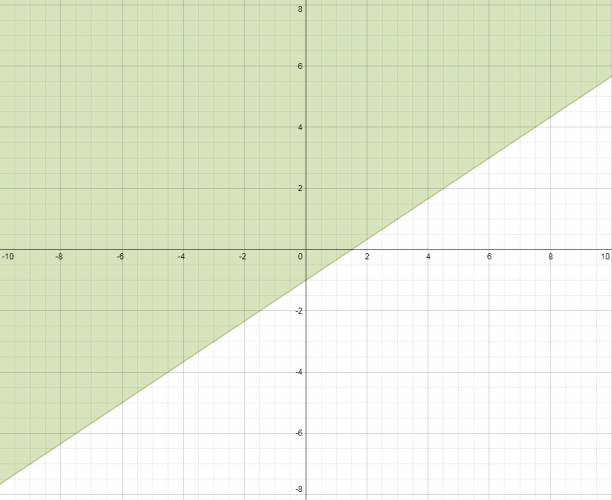 y ≤ -3·x + 8: 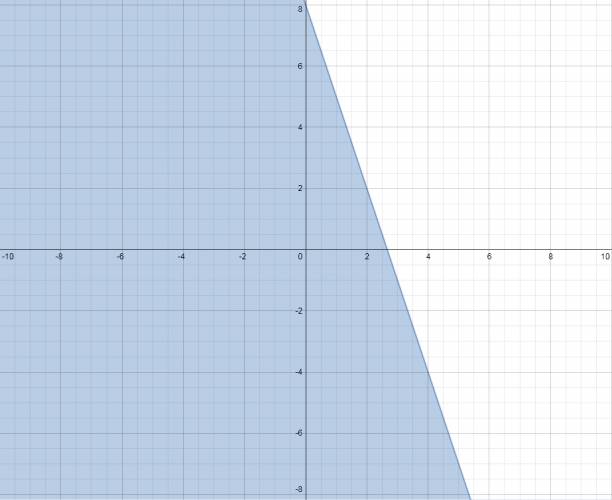 Todas las anteriores inecuaciones representadas gráficamente: 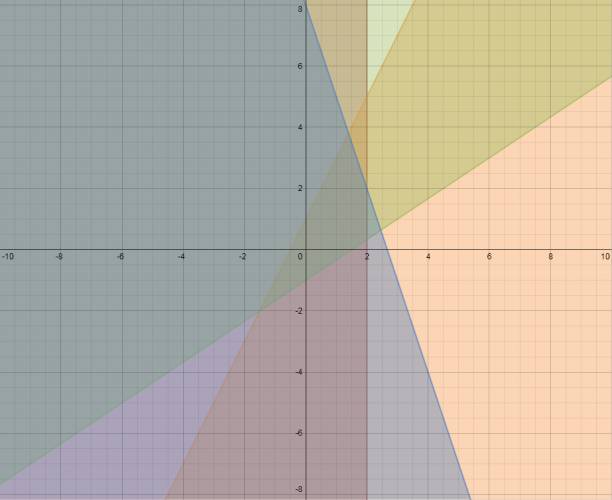 La solución gráfica del sistema es: 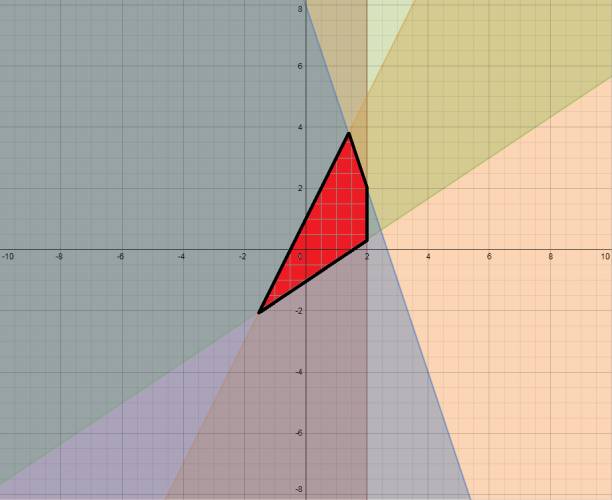 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |







