|
| Foro Departamento de Matemática Problemas resueltos Estudiar funciones racionales |
| Estudiar funciones racionales |
|
06-03-2013, 10:56 PM (Este mensaje fue modificado por última vez por: marcos364 - Miércoles, 06-03-2013, 10:57 PM.)
Post: #1
|
|||
|
|||
|
1. $$ f(x) = \frac {1}{(x-2)·(x+1)·(x+3)} $$
2. $$ f(x) = \frac {2·x+1}{x^2 - 9} $$ 3. $$ f(x) = \frac {2·x+1}{(x-4)·(x-2)·(x+3)} $$ 4. $$ f(x) = \frac {x+6}{x^2 - x - 20} $$ 5. $$ f(x) = \frac {1}{x^2} $$ 6. $$ f(x) = \frac {4·x - 2}{4·x^2 - 6·x + 8·(x+3)} $$ |
|||
|
06-03-2013, 11:03 PM
Post: #2
|
|||
|
|||
|
Primera:
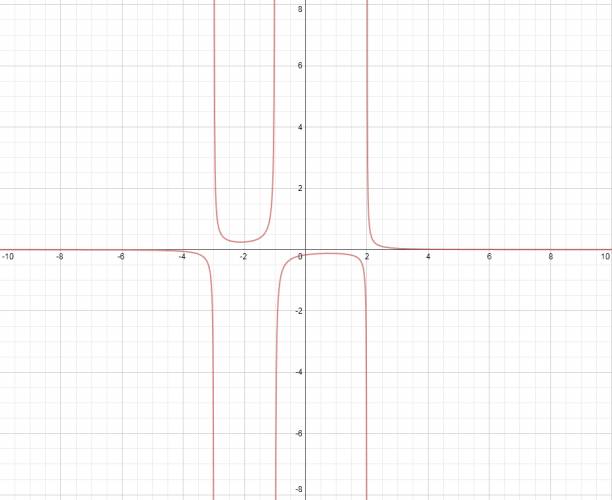
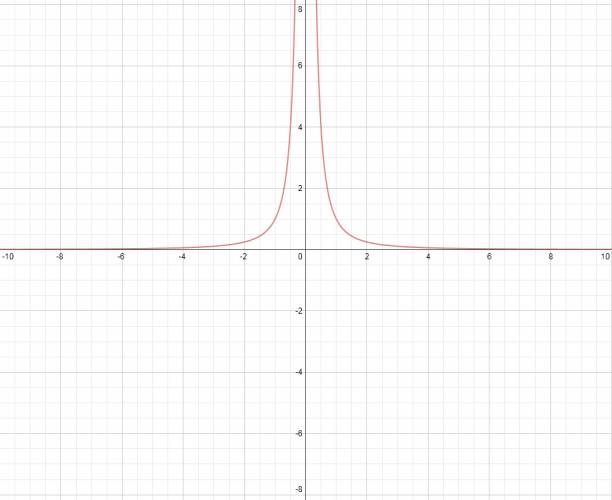
$$ f(x) = \frac {1}{(x-2)·(x+1)·(x+3)} $$ Lo primero sería hallar las raíces, pero la función no corta el eje \( x \), por lo que no las tiene, esto lo sé ya que no hay ninguna ecuación en el numerador. Estudio de la existencia: Igualamos a 0 todo el denominador: $$ (x-2)·(x+1)·(x+3) = 0 $$ Por la propiedad Hankeliana, podemos igualar cada factor a 0. $$ x - 2 = 0 ⇒ x = 2 $$ $$ x + 1 = 0 ⇒ x = - 1 $$ $$ x + 3 = 0 ⇒ x = -3 $$ Lo que hicimos fue hallar todo los número que hacían que el denominador fuera 0, pero si recordamos: el denominador de una fracción nunca puede valer 0. Por lo que el dominio de la función es: \( D = ℝ - \left\{ -3,-1,2 \right\} \). Una representación gráfica de la función es: Como podemos ver, hay asíntotas en: $$ x = 2 $$ $$ x = -3 $$ $$ x = 1 $$ Son los mismos números que hemos quitado del dominio. También tiene una asíntota horizontal en \( y = 0 \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-03-2013, 11:11 PM
Post: #3
|
|||
|
|||
|
Segunda:
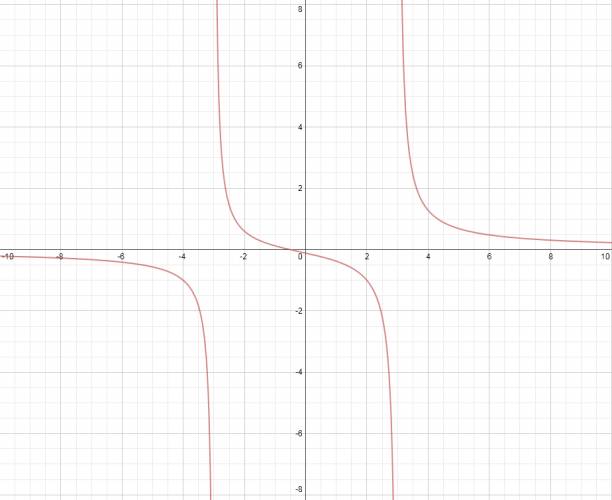
$$ f(x) = \frac {2·x+1}{x^2 - 9} $$ Esta función sí tiene raíces, por lo que vamos a hallarlas, esto lo hacemos igualando el numerador a 0. $$ 2·x+1 = 0 ⇒ 2·x = - 1 ⇒ x = \frac {-1}{2} $$ Esto significa que va a corta el eje \( x \) en ese punto. Estudio de la existencia: Se hace igualando el denominador a 0: $$ x^2 - 9 = 0 ⇒ x^2 = 9 ⇒ x = ± \sqrt {9} ⇒ x = ± 3 $$ Como hicimos en el caso anterior, restamos estos números al dominio, allí habrán asíntotas. $$ D = ℝ - \left\{ -3, +3 \right\} $$ La gráfica: Este tema siempre se da antes de dar límites, por lo cual no voy a explicar cómo se calcula el límite de la función, simplemente voy a decir que la función tiene otra asíntota horizontal en \( y = 0 \), como bien se puede apreciar en el gráfico. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-03-2013, 11:35 PM
Post: #4
|
|||
|
|||
|
Tercera:
$$ f(x) = \frac {2·x+1}{(x-4)·(x-2)·(x+3)} $$ Raíces: $$ 2·x+1 = 0 ⇒ 2·x = - 1 ⇒ x = \frac {-1}{2} $$ Estudio de la existencia: $$ (x-4)·(x-2)·(x+3) = 0 $$ $$ x - 4 = 0 ⇒ x = 4 $$ $$ x - 2 = 0 ⇒ x = 2 $$ $$ x + 3 = 0 ⇒ x = - 3 $$ Asíntotas: · Vertical en: \( x=4, x=2, x=-3 \). · Horizontal en: \( y = 0 \). Gráfica: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-03-2013, 11:39 PM
Post: #5
|
|||
|
|||
|
Cuarta:
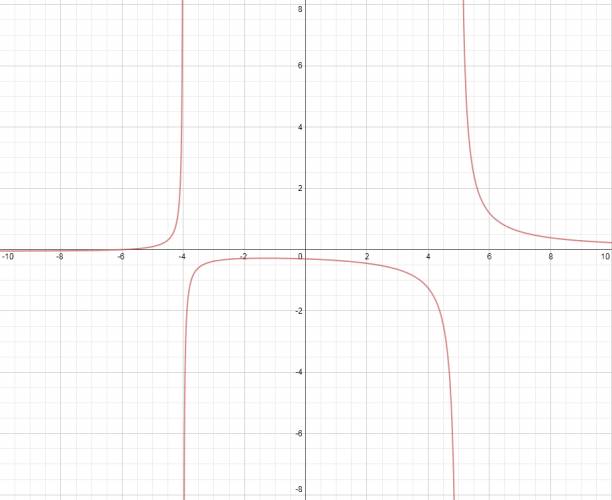
$$ f(x) = \frac {x+6}{x^2 - x - 20} $$ Raíces: $$ x+6 = 0 ⇒ x = -6 $$ Existencia: $$ x^2 - x - 20 = 0 ⇒ x=5, x=-4 $$ Asíntotas: · Vertical en: \( x=5, x=-4 \) · Horizontal en: \( y = 0 \) Gráfica: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-03-2013, 11:41 PM
Post: #6
|
|||
|
|||
|
Quinta:
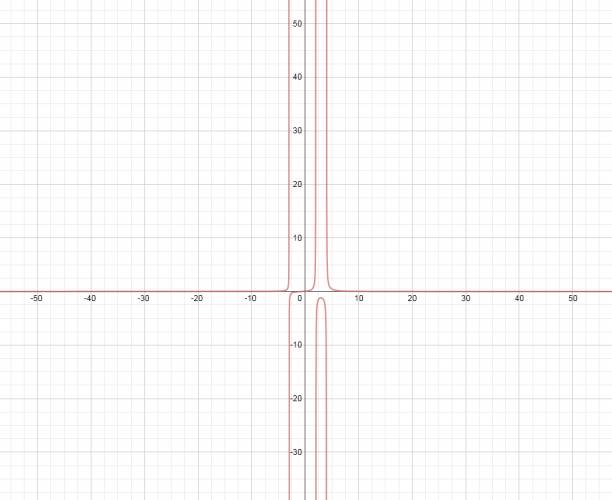
$$ f(x) = \frac {1}{x^2} $$ Raíces: No tiene. Existencia: $$ x^2 = 0 ⇒ x = 0 (doble) $$ Asíntotas: Son los propios ejes. Gráfica: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-03-2013, 11:46 PM
Post: #7
|
|||
|
|||
|
Sexta:
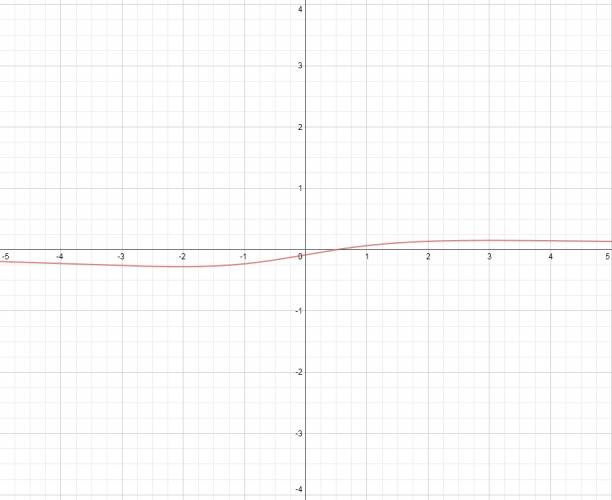
$$ f(x) = \frac {4·x - 2}{4·x^2 - 6·x + 8·(x+3)} $$ Raíces: $$ 4·x - 2 = 0 ⇒ 4·x = 2 ⇒ x = \frac {2}{4} ⇒ x = \frac {1}{2} $$ Existencia: $$ 4·x^2 - 6·x + 8·(x+3) = 0 ⇒ 4·x^2 - 6·x + 8·x+ 24 = 0 ⇒ 4·x^2 + 2·x+ 24 = 0 ⇒ $$ no tiene raíces reales. Gráfica: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |