| Foro Departamento de Matemática Problemas resueltos Problemas Matemáticos (Sistemas de Ecuaciones-Función Lineal |
| Problemas Matemáticos (Sistemas de Ecuaciones-Función Lineal |
|
31-01-2013, 4:43 AM
Post: #1
|
|||
|
|||
|
1) Elige la opción correcta
a) Marcelo gana un sueldo de $2500 más una comisión del 6,5% sobre sus ventas totales del mes. Si cobró $4775. Sus ventas totales del mes fueron: a. 3500 b. 350 c. 35000 d. 350000 e. Ninguna de las anteriores b) La suma de las edades de tres personas es 88 años. La mayor tiene 20 años más que la menor y la de en medio 18 años menos que la mayor. Las respectivas edades son: a. 44, 26, 24 b. 42, 24, 22 c. 40, 22, 20 d.48, 20, 20 e. Ninguna de las anteriores 2) El valor de x en la siguiente ecuación es: 2-1) (x+1)/5 = (3x-9)/3 a. 3 b. 1 c. 2/3 d. 4 e. Ninguna de las anteriores 2-2) (x + 7)(2x - 1) = 0 a. x1=2 ; x2= 7 b. x1=-2 ; x2= 7 c. x1= -2 ; x2= - 7 d. x1=2 ; x2= -7 e. Ninguna de las anteriores 3) La ecuación de la recta que pasa por el punto (0,-4) y es perpendicular a la recta: 2x + y + 3 = 0, es: a. -x+2y - 4=0 b. - ½ x +y +4=0 c. ½ x - y - 4 =0 d. 2x + y+ 4 =0 e. Ninguna de las anteriores 4) La solución del siguiente sistema de ecuaciones es: 1/2x -1/5y = 3/2 { 2/3x + 1/4y = 5/12 a) (103/31 , 26/31) b) (17/5 , 1) c) infinitas d) vacía e) Ninguna de las anteriores 5) El resultado de la siguiente integral, es: S (sub 1) (al cubo) (2x (al cuadrado) +3) a) 16/3 b) 32/3 c) 16 e) Ninguna de las anteriores Nota: La "S" del integral, es la "ese" alargada. Perdonen que aún no entiendo bien como manejar los simbolos en el foro, pero ya le agarrare la mano para colocarlos uno por uno Estos ejercicios me vendrán bien para la práctica y resolución de ejercicios, y procedimientos. Agradezco mucho de la ayuda que puedan brindarme Muchas Gracias. |
|||
|
31-01-2013, 5:31 AM
Post: #2
|
|||
|
|||
|
Hola Ovale,
Sé bienvenido al foro, pónte un avatar. Temo que es realmente tarde, y me tengo que levantar en poco más de un par de horas, pero prometo ayudarte con tus ejercicios más tarde, mientras tanto siéntete libre de publicar más ejercicios y de ver como he resuelto algunos. Por otro lado me interesaría saber cómo has llegado al foro, y específicamente qué nivel de estudios estás cursando, para ver por dónde puedo orientar mis respuestas. Saludos.  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 7:10 AM
Post: #3
|
|||
|
|||
|
Gracias por la bienvenida.
Llegue al foro creo que por yahoo respuestas, un link me redireccionó aqui. Ademas, que en un tema anterior, me han resuelto ejercicios de Física que me sirvieron de mucho para el estudio. Fue hace unos meses, si encuentro el enlace del tema, lo dejare. Pasé al 5to año del secundario, y para el año próximo empezare a cursar ingeniería Agradezco el tiempo y trabajo en tomarse para responder. A mi me ayuda de mucho |
|||
|
31-01-2013, 8:36 AM
Post: #4
|
|||
|
|||
|
Me alegra mucho que el foro sea de utilidad de todos. Y siempre es curioso saber de dónde vienen los visitantes.
 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 8:45 AM
Post: #5
|
|||
|
|||
|
Bien, comencemos:
Primer problema: Quote (Ovale) Marcelo gana un sueldo de $2500 más una comisión del 6,5% sobre sus ventas totales del mes. Si cobró $4775. Marcelo tenga o no ventas ganará $2.500, pero la comisión que es de un 6,5% depende de las ventas que realice, cuantas más ventas concrete, mayor será el sueldo. Esto lo podemos expresar como una ecuación: $$ 2.500 + (6,5 \%)·x = 4.775 $$ Quote Truco: Por ejemplo el 90% de algo, es escribir \( \frac {90}{100} \) y multiplicarlo por este algo, esto haré con la ecuación anterior, atento. $$ 2.500 + \frac {6,5}{100} ·x = 4.775 ⇒ 2.500 + 0,065 ·x = 4.775 $$ Ahora voy a despejar: primero me saco los que están sumando o restando y luego los que están multiplicando o dividiendo. $$ 2.500 + 0,065 ·x = 4.775 ⇒ 0,065 ·x = 4.775 - 2.500 ⇒ 0,065 ·x = 2.275 $$ $$ 0,065 ·x = 2.275 ⇒ \frac {2.275}{0,065} = 35.000 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 8:53 AM
Post: #6
|
|||
|
|||
|
Primer problema, segunda parte:
Quote (Ovale) La suma de las edades de tres personas es 88 años. La mayor tiene 20 años más que la menor y la de en medio 18 años menos que la mayor. Con esta información voy a armar un sistema de ecuaciones de 3 x 3: $$ \begin{cases} a+b+c=88 \\ a=20+c \\ b=a-18 \end{cases} $$ Despejo \( a \) en la tercer ecuación: $$ b = a - 18 ⇒ -a = -b - 18 ⇒ a = b + 18 $$ Igualo la segunda y la tercer ecuación, y despejo \( b \): $$ b + 18 = 20 + c ⇒ b = 20 - 18 + c ⇒ b = 2 + c $$ Reemplazo en la primer ecuación la segunda ecuación y la que acabo de despejar: $$ a + b + c = 88 ⇒ (20 + c) + (2 + c) + c = 88 ⇒ 3·c + 22 = 88 ⇒ 3·c = 88 - 22 ⇒ 3·c = 66 ⇒ c = \frac {66}{3} = 22 $$ Reemplazo el valor de \( c \) en la segunda ecuación: $$ a = 20 + c ⇒ a = 20 + 22 ⇒ a = 42 $$ Reemplazo el valor de \( a \) en la tercer ecuación: $$ b = a -18 ⇒ b = 42 - 18 ⇒ b = 24 $$ $$ S = \left\{ 42; 24; 22 \right\} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 9:19 AM
Post: #7
|
|||
|
|||
|
Segundo problema:
Quote (Ovale) (x+1)/5 = (3x-9)/3 $$ \frac {x+1}{5} = \frac {3·x-9}{3} $$ Antes que nada, podemos realizar la división del segundo miembro: $$ \frac {x+1}{5} = x - 3 $$ Como todo en matemática, se puede hacer de varias formas, pero uno siempre tiene que tratar de resolverlo por el método más rápido y más fácil, por lo cual aplicaré una propiedad. Quote Propiedad de las fracciones iguales o equivalentes: Dos fracciones son equivalentes o iguales si sus productos cruzados son iguales. $$ \frac {a}{b} = \frac {c}{d} ⇔ a·d = b·c $$ Recordar que: $$ \frac {x+1}{5} = x - 3 ⇔ \frac {x+1}{5} = \frac {x - 3}{1} $$ Aplico la propiedad y multiplico cruzado, sin ningún tipo de problemas. $$ (x+1)·1 = 5·(x-3) $$ Desarrollamos: aplicamos distributiva, juntamos términos semejantes y despejamos: $$ x + 1 = 5·x - 15 ⇒ 5·x - x = 15 + 1 ⇒ 4·x = 16 ⇒ x = \frac {16}{4} = 4 $$ Verificación: $$ \frac {x+1}{5} = x - 3 $$ $$ \frac {4+1}{5} = 4 - 3 $$ $$ \frac {5}{5} = 1 $$ $$ 1 = 1 $$ Se verifica la igualdad. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 9:27 AM
Post: #8
|
|||
|
|||
|
Segundo problema, segunda parte:
Quote (Ovale) (x + 7)(2x - 1) = 0 $$ (x + 7)·(2·x - 1) = 0 $$ Podríamos desarrollar todo el polinomio y resolver por la fórmula de Bháskara, o podemos aplicar una forma más sencilla. Aplicamos la propiedad Hankeliana del producto. Quote Propiedad Hankeliana del producto: Si el producto de dos números es cero es porque al menos uno de ellos lo es. $$ a·b = 0 ⇔ a=0 ∨ b=0 $$ Para que el resultado de tal multiplicación sea cero es necesario que al menos uno de los paréntesis dé cero, por esto igualamos cada factor a cero. $$ x + 7 = 0 ⇒ x = -7 $$ $$ 2·x - 1 = 0 ⇒ 2·x = 1 ⇒ x = \frac {1}{2} $$ $$ S = \left\{ \frac {1}{2}; -7 \right\} $$ Verificación: Si \( x = -7 \): $$ (x + 7)·(2·x - 1) = 0 $$ $$ (-7 + 7)·(2·(-7) - 1) = 0 $$ $$ (0)·(-14 - 1) = 0 $$ $$ 0 = 0 $$ Si \( x = \frac {1}{2} \): $$ (x + 7)·(2·x - 1) = 0 $$ $$ (\frac {1}{2} + 7)·(2·\frac {1}{2} - 1) = 0 $$ $$ (\frac {1}{2} + 7)·(1 - 1) = 0 $$ $$ (\frac {1}{2} + 7)·(0) = 0 $$ $$ 0 = 0 $$ Se verifican ambos valores en la igualdad. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 9:40 AM
Post: #9
|
|||
|
|||
|
Tercer problema:
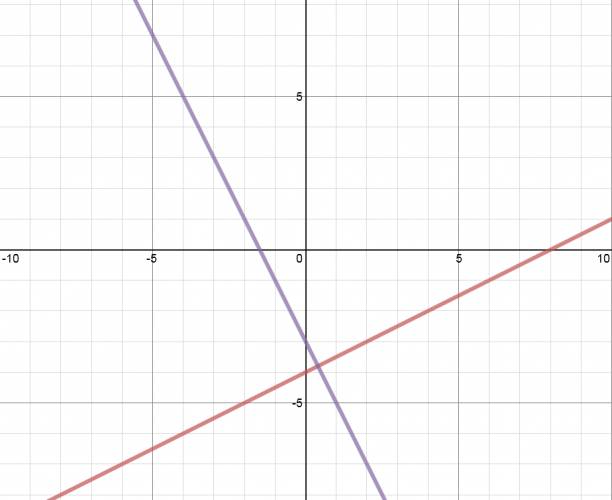
Quote (Admin) La ecuación de la recta que pasa por el punto (0,-4) y es perpendicular a la recta: 2x + y + 3 = 0 Comencemos pasando la ecuación del problema de la forma general a la explícita (dejar la \( y \) sola de un lado): $$ 2·x + y + 3 = 0 ⇒ y = -2·x - 3 $$ Recordemos la condición de perpendicularidad: Quote Condición de perpendicularidad: Dos rectas son perpendicular si el producto de sus pendientes da el opuesto de la unidad. $$ m·m' = -1 $$ La anterior recta tiene \( m = -2 \); ahora resolvemos: $$ -2·m' = -1 ⇒ m' = \frac {1}{2} $$ Ahora partimos de la forma de la ecuación de la recta, y sustituimos lo que conocemos: $$ y = m·x + n $$ $$ y = \frac {1}{2}·x + n $$ Quote A tener en cuenta: Si me dicen que una recta pasa por un punto \( A (x,y) \), me están dando los valores de \( x \) y \( y \) para sustituirlos en la ecuación de la fórmula. $$ -4 = \frac {1}{2}·0 + n $$ $$ -4 = 0 + n $$ $$ n = -4 $$ La ecuación de la recta buscada es: $$ y = \frac {1}{2}·x - 4 $$ Me he tomado la molestia de graficar las rectas para entender mejor el problema: $$ y = \frac {1}{2}·x - 4 $$ $$ y = -2·x - 3 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
31-01-2013, 9:46 AM
Post: #10
|
|||
|
|||
|
Cuarto problema:
$$ \begin{cases} \frac {1}{2}·x - \frac {1}{5}·y = \frac {3}{2} \\ \frac {2}{3}·x + \frac {1}{4}·y = \frac {5}{12} \end{cases} $$ A mí personalmente no me gusta trabajar con las fracciones, por lo que pasaré a las dos ecuaciones a número enteros así es más fácil trabajar. Quote Truco: Para deshacernos de los denominadores de una ecuación, debemos hallar un número que sea múltiplo de todos ellos y finalmente multiplicar la todos los términos de la ecuación por este. Primera ecuación: Multiplico todos los términos por 10. $$ \frac {1}{2}·x - \frac {1}{5}·y = \frac {3}{2} ⇒ 5·x - 2·y = 15 $$ Segunda ecuación: Multiplico todos los términos por 12. $$ \frac {2}{3}·x + \frac {1}{4}·y = \frac {5}{12} ⇒ 8·x + 3·y = 5 $$ Formo nuevamente el sistema: $$ \begin{cases} 5·x - 2·y = 15 \\ 8·x + 3·y = 5 \end{cases} $$ Como las ecuaciones y el sistema en sí no tienen nada raro lo puedo resolver por reducción, el cual para mí, es el método más rápido. Para quitarnos \( x \): Multiplico la primera ecuación por \( -8 \): $$ 5·x - 2·y = 15 ⇒ -40·x + 16·y = -120 $$ Multiplico la segunda ecuación por \( 5 \): $$ 8·x + 3·y = 5 ⇒ 40·x + 15·y = 25 $$ Las sumamos: $$ { -40·x + 16·y = -120 \atop \underline{40·x + 15·y = 25}} $$ $$ 31·y = -95 $$ Despejamos la anterior ecuación: $$ 31·y = -95 ⇒ y = - \frac {95}{31} $$ La fracción es irreducible. Para quitarnos \( y \): Multiplico la primera ecuación por \( 3 \): $$ 5·x - 2·y = 15 ⇒ 15·x-6·y= 45 $$ Multiplico la segunda ecuación por \( 2 \): $$ 8·x + 3·y = 5 ⇒ 16·x + 6·y = 10 $$ Las sumamos: $$ { 15·x-6·y= 45 \atop \underline{16·x + 6·y = 10}} $$ $$ 31·x = 55 $$ Despejamos: $$ 31·x = 55 ⇒ x = \frac {55}{31} $$ La fracción es irreducible. $$ S = \left\{ \frac {55}{31}; - \frac {95}{31} \right\} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |