|
| Foro Departamento de Física Problemas sin resolver Varios problemas de movimiento en dos dimensiones |
| Varios problemas de movimiento en dos dimensiones |
|
30-03-2013, 2:33 AM
Post: #1
|
|||
|
|||
|
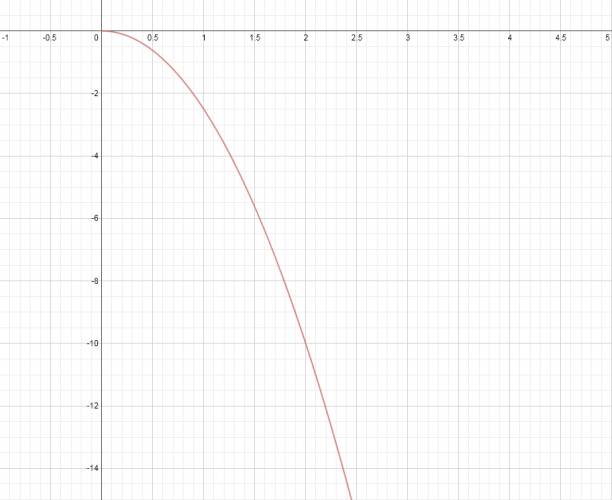
1. El gráfico que se muestra, corresponde a la velocidad en función del tiempo de un cuerpo lanzado verticalmente hacia arriba. Determine los instantes \( t_{1} \) y \( t_{2} \). Considere \( g = 10 \frac {m}{s^2} \).
 2. Un avión suelta una bomba en “o”. Deduzca la ecuación de la trayectoria de la bomba, respecto al sistema referencial planteado, suponiendo que la velocidad del avión es conocida. 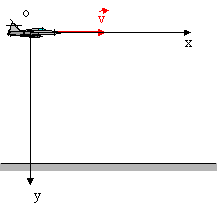 3. Determinar el alcance del proyectil y la velocidad inicial, sabiendo que \( v_{H} = 6,0 \frac {m}{s} \) y \( h = 3,2 m \). Considere \( g = 10 \frac {m}{s^2} \). 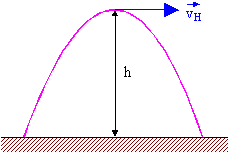 4. Una bolita, tras rodar sobre una mesa horizontal, cae. Determine la velocidad con que llega al piso si, desde que abandonó la mes, la componente horizontal del desplazamiento vale \( 1,2 m \) y el tiempo de vuelo \( 0,4 s \). 5. Un golfista se encuentra en la cima de una colina a 50 m horizontales del hoyo y 5,0 m de altura. Elige un palo que hace que la pelota salga disparada con un ángulo de 45º respecto a la horizontal. Determine la velocidad que debe imprimirle a la pelota, para que caiga justo dentro del hoyo. 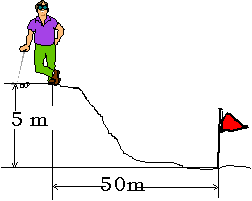 6. Un proyectil es lanzado con una velocidad inicial que forma un ángulo de 60º hacia arriba, de forma tal que cuando alcanza el punto de máxima altura, su velocidad es \( 2,0 \frac {m}{s} \). Determine la velocidad inicial. |
|||
|
30-03-2013, 2:53 AM
Post: #2
|
|||
|
|||
|
Quote (marcos364) 1. El gráfico que se muestra, corresponde a la velocidad en función del tiempo de un cuerpo lanzado verticalmente hacia arriba. Determine los instantes t1 y t2. Considere g=10ms2. Sabemos que la \( v_{o} = 20 \frac {m}{s} \), por el gráfico: 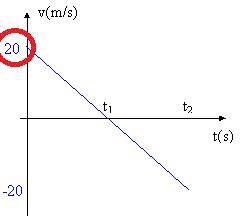 Vamos hallar \( t_{1} \) que es cuando \( v = 0 \frac {m}{s} \): $$ v_{f} = v_{o} - g·\Delta t ⇒ 0 \frac {m}{s} = 20 \frac {m}{s} - 10 \frac {m}{s^2}·\Delta t_{1} ⇒ -20 \frac {m}{s} = \Delta t_{1} ⇒ \Delta t_{1} = \frac {-20 \frac {m}{s}}{-10 \frac {m}{s^2}} ⇒ \Delta t_{1} = 2,0 s $$ Vamos hallar \( t_{2} \) que es cuando \( v = 0 \frac {m}{s} \): $$ v_{f} = v_{o} - g·\Delta t ⇒ - 20 \frac {m}{s} = 20 \frac {m}{s} - 10 \frac {m}{s^2}·\Delta t_{2} ⇒ -40 \frac {m}{s} = \Delta t_{2} ⇒ \Delta t_{2} = \frac {420 \frac {m}{s}}{-10 \frac {m}{s^2}} ⇒ \Delta t_{2} = 4,0 s $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
30-03-2013, 3:03 AM
Post: #3
|
|||
|
|||
|
Quote (marcos364) 2. Un avión suelta una bomba en “o”. Deduzca la ecuación de la trayectoria de la bomba, respecto al sistema referencial planteado, suponiendo que la velocidad del avión es conocida. Vemos que el gráfico es \( x(t) \), por lo que tenemos que deducir una fórmula que presente de un lado del signo de igual: una variable de posición en horizontal y del otro lado, una variable de posición vertical. Como vemos, el avión viaja con una velocidad horizontal, por lo que \( v_{oy} = 0 \). Como recordaremos, en proyectiles, \( v_{x} \) mantiene un movimiento constante (MRU). Despejemos su única fórmula para la variable tiempo: $$ v_{x} = \frac {\Delta x}{\Delta t} ⇒ \Delta t = \frac {\Delta x}{v_{x}} $$ Si recordamos, en vertical, los proyectiles se mueven con un movimiento variado (MRUV), despejemos su fórmula de altura: $$ \Delta y = -\frac {g·\Delta t^2}{2} $$ Reemplazamos el tiempo de la primera: $$ \Delta y = -\frac {g·(\frac {\Delta x}{v_{x}})^2}{2} $$ Reemplazamos por los datos que conocemos: $$ \Delta y = -\frac {10 \frac {m}{s^2}·(\frac {\Delta x}{v_{x}})^2}{2} ⇒ \Delta y = -5 ·\frac {\Delta x^2}{v_{x}^2} $$ La velocidad es variable pero el problema dice que es conocido, para verificar que esté correcto, voy a dar un valor cualquiera, por ejemplo: \( v_{x} = 2,0 \frac {m}{s} \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |