30-03-2013, 2:33 AM
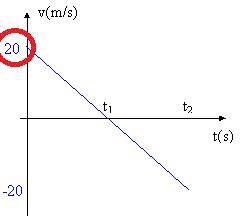
1. El gráfico que se muestra, corresponde a la velocidad en función del tiempo de un cuerpo lanzado verticalmente hacia arriba. Determine los instantes \( t_{1} \) y \( t_{2} \). Considere \( g = 10 \frac {m}{s^2} \).

2. Un avión suelta una bomba en “o”. Deduzca la ecuación de la trayectoria de la bomba, respecto al sistema referencial planteado, suponiendo que la velocidad del avión es conocida.
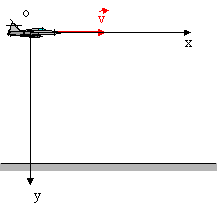
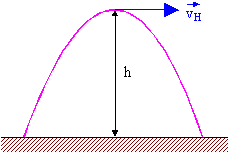
3. Determinar el alcance del proyectil y la velocidad inicial, sabiendo que \( v_{H} = 6,0 \frac {m}{s} \) y \( h = 3,2 m \). Considere \( g = 10 \frac {m}{s^2} \).
4. Una bolita, tras rodar sobre una mesa horizontal, cae. Determine la velocidad con que llega al piso si, desde que abandonó la mes, la componente horizontal del desplazamiento vale \( 1,2 m \) y el tiempo de vuelo \( 0,4 s \).
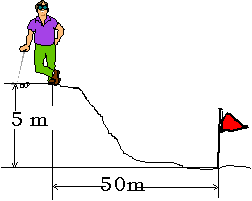
5. Un golfista se encuentra en la cima de una colina a 50 m horizontales del hoyo y 5,0 m de altura. Elige un palo que hace que la pelota salga disparada con un ángulo de 45º respecto a la horizontal. Determine la velocidad que debe imprimirle a la pelota, para que caiga justo dentro del hoyo.
6. Un proyectil es lanzado con una velocidad inicial que forma un ángulo de 60º hacia arriba, de forma tal que cuando alcanza el punto de máxima altura, su velocidad es \( 2,0 \frac {m}{s} \). Determine la velocidad inicial.

2. Un avión suelta una bomba en “o”. Deduzca la ecuación de la trayectoria de la bomba, respecto al sistema referencial planteado, suponiendo que la velocidad del avión es conocida.

3. Determinar el alcance del proyectil y la velocidad inicial, sabiendo que \( v_{H} = 6,0 \frac {m}{s} \) y \( h = 3,2 m \). Considere \( g = 10 \frac {m}{s^2} \).

4. Una bolita, tras rodar sobre una mesa horizontal, cae. Determine la velocidad con que llega al piso si, desde que abandonó la mes, la componente horizontal del desplazamiento vale \( 1,2 m \) y el tiempo de vuelo \( 0,4 s \).
5. Un golfista se encuentra en la cima de una colina a 50 m horizontales del hoyo y 5,0 m de altura. Elige un palo que hace que la pelota salga disparada con un ángulo de 45º respecto a la horizontal. Determine la velocidad que debe imprimirle a la pelota, para que caiga justo dentro del hoyo.

6. Un proyectil es lanzado con una velocidad inicial que forma un ángulo de 60º hacia arriba, de forma tal que cuando alcanza el punto de máxima altura, su velocidad es \( 2,0 \frac {m}{s} \). Determine la velocidad inicial.