|
| Foro Departamento de Física Problemas sin resolver Problemas de movimiento (mezclados los de MRU con MRUV) |
| Problemas de movimiento (mezclados los de MRU con MRUV) |
|
22-03-2013, 0:35 AM
Post: #1
|
|||
|
|||
|
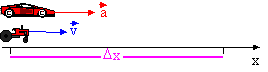
1. En el instante que un automóvil parte del reposo con aceleración constante de \( 2,0 \frac {m}{s^2} \), otro automóvil pasa a su lado con velocidad constante de \( 10 \frac {m}{s} \). Calcular al cabo de cuanto tiempo, el primero vuelve a alcanzar al segundo y que velocidad tendrá en ese momento el primer auto.
 2. Una esfera se encuentra en el techo de un vagón que parte del reposo con aceleración constante de \( 5,0 \frac {m}{s^2} \) como muestra la figura. Determinar a que distancia se encuentra del vagón, cuando la esfera llega al piso si la altura inicial es de \( 5,0 m \). 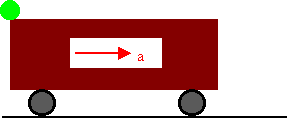 3. El gráfico adjunto, corresponde a la aceleración en función del tiempo de un móvil con trayectoria rectilínea. Realizar el gráfico de la velocidad en función del tiempo sabiendo que la velocidad inicial es cero, y calcule la distancia recorrida por el móvil. 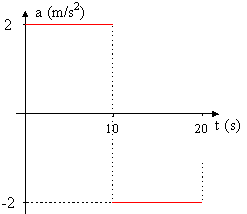 4. La velocidad de un móvil, en movimiento rectilíneo experimenta la variación indicada por el gráfico. Calcular la aceleración media desde \( t = 0 s \) a \( t = 5 s \) y dibujar el gráfico de la aceleración en función del tiempo. 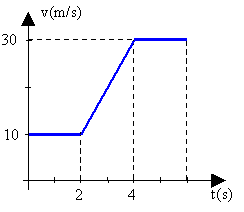 5. El gráfico adjunto, muestra la gráfica de la velocidad en función del tiempo, de un objeto que se mueve en una trayectoria rectilínea. Sabiendo que después del instante \( t = 10 s \), el módulo de la aceleración es el doble que antes, determine el instante de tiempo final en el cual la velocidad es cero. 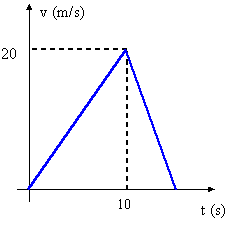 6. Una pelota se lanza verticalmente hacia arriba, con velocidad inicial \( v_{o} \). Realizar el gráfico de la velocidad en función del tiempo, desde que es lanzada hasta que vuelve a la misma altura donde se soltó. 7. Un cuerpo es lanzado verticalmente hacia arriba con una velocidad de \( 50 \frac {m}{s^2} \). Realice el gráfico de velocidad instantánea en función del tiempo para los primeros \( 10 s \) desde el lanzamiento. 8. En la figura vemos el gráfico de la posición en función del tiempo, para un cuerpo que se mueve en línea recta. Realice la gráfica de la velocidad en función del tiempo. 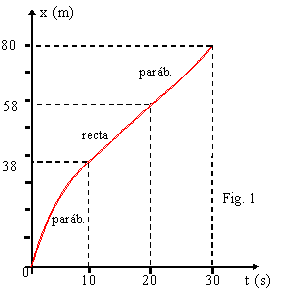 9. Un objeto se mueve sobre una línea recta, de manera que la velocidad varía en función del tiempo, como indica el gráfico. Hallar: el desplazamiento máximo y la aceleración. 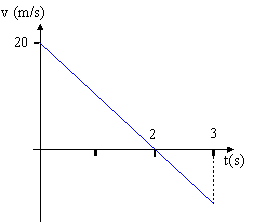 10. El gráfico adjunto representa la velocidad en función del tiempo, de un objeto que se mueve en una trayectoria rectilínea. Sabiendo que a partir de \( t = 10 s \), el módulo de la aceleración, es el doble del que hay entre cero y diez segundos, determine \( t_{f} \).  11. La gráfica adjunta, muestra la aceleración de un cuerpo con movimiento rectilíneo en función del tiempo. Sabiendo que la velocidad inicial es cero y parte del reposo, trazar la gráfica de la velocidad en función del tiempo y de la posición en función del tiempo. 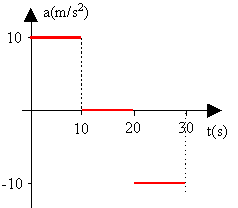 12. Un cuerpo se mueve en una trayectoria rectilínea. En el instante \( t_{o} = 0 s\), su velocidad es \( 4,0 \frac {m}{s^2} \) y su aceleración es cero, hasta el instante \( t = 2 s \) en el que se le imprime una aceleración constante de sentido opuesto a la velocidad y módulo \( 5,0 \frac {m}{s^2} \), retornando a la posición que tenía en el instante \( t_{o} \). Realice el gráfico \( v = f(t) \) entre los instantes \( t_{o} \) y \( t_{f} \). |
|||
|
24-03-2013, 0:18 AM
Post: #2
|
|||
|
|||
|
Quote (marcos364) 1. En el instante que un automóvil parte del reposo con aceleración constante de 2,0ms2, otro automóvil pasa a su lado con velocidad constante de 10ms. Calcular al cabo de cuanto tiempo, el primero vuelve a alcanzar al segundo y que velocidad tendrá en ese momento el primer auto. Básicamente podemos considerar que ambos móviles parten al mismo tiempo. Vamos a considerar los dós móviles por separado para facilitar su estudio. MÓVIL 1: \( v_{o} = 0 \frac {m}{s} \) \( a = 2,0 \frac {m}{s^2} (cte) \) Como actúa la aceleración estamos en presencia de un movimiento variado (o acelerado). Como nos piden que hallemos el desplazamiento en que se encuentran, simplemente vamos a plantear la fórmula de desplazamiento del movimiento variado. $$ \Delta x = v_{o}·\Delta t + \frac {a·\Delta t^2}{2} $$ $$ \Delta x = (0 \frac {m}{s})·\Delta t + \frac {2,0 \frac {m}{s^2}·\Delta t^2}{2} $$ $$ \Delta x = \Delta t^2 $$ MÓVIL 2: \( v_{o} = 10 \frac {m}{s} (cte) \) Como no actúa la aceleración estamos en presencia de un movimiento uniforme. Como nos piden que hallemos el desplazamiento en que se encuentran, simplemente vamos a plantear la fórmula de desplazamiento del movimiento rectilíneo uniforme. $$ v_{x} = \frac {\Delta x}{\Delta t} ⇒ \Delta x = v_{x}·\Delta t $$ $$ \Delta x = (10 \frac {m}{s})·\Delta t $$ De modo que igualamos para hallar el tiempo: $$ \Delta t^2 = (10 \frac {m}{s})·\Delta t ⇒ \Delta t^2 - (10 \frac {m}{s})·\Delta t = 0 $$ Resolvemos y llegamos a que: $$ \Delta t_{1} = 0 s ⇒ \Delta t_{2} = 10 s $$ El \( \Delta t_{1} \) ya lo sabíamos por en un principio el problema nos dice que se cruzan y nos preguntan cuándo se vuelven a cruzar, por lo que esto es algo redundante. Sustituimos en cualquiera de las dos ecuaciones que planteamos y podemos conocer el desplazamiento. Como se encuentran en un mismo punto, nos va a dar los mismo resolvamos cualquiera de las dos. Para orientar a los perdidos voy a sustituir y resolver para las dos: MÓVIL 1: $$ \Delta x = \Delta t^2 ⇒ \Delta x = (10 s)^2 ⇒ \Delta x = 100 m $$ MÓVIL 2: $$ \Delta x = (10 \frac {m}{s})·\Delta t ⇒ \Delta x = (10 \frac {m}{s})·(10 s) ⇒ \Delta x = 100 m $$ Ahora nos piden que calculemos cuál será la velocidad del primer móvil en el momento de encuentro. Recordemos que: $$ v_{f} = v_{o} + a·\Delta t ⇒ v_{f} = 0 \frac {m}{s} + 2,0 \frac {m}{s^2}·(10 s) ⇒ v_{f} = 20 \frac {m}{s} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |







