22-03-2013, 0:35 AM
1. En el instante que un automóvil parte del reposo con aceleración constante de \( 2,0 \frac {m}{s^2} \), otro automóvil pasa a su lado con velocidad constante de \( 10 \frac {m}{s} \). Calcular al cabo de cuanto tiempo, el primero vuelve a alcanzar al segundo y que velocidad tendrá en ese momento el primer auto.
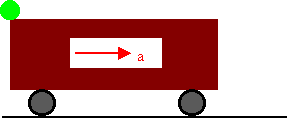
2. Una esfera se encuentra en el techo de un vagón que parte del reposo con aceleración constante de \( 5,0 \frac {m}{s^2} \) como muestra la figura. Determinar a que distancia se encuentra del vagón, cuando la esfera llega al piso si la altura inicial es de \( 5,0 m \).
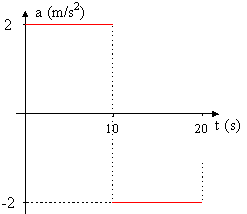
3. El gráfico adjunto, corresponde a la aceleración en función del tiempo de un móvil con trayectoria rectilínea. Realizar el gráfico de la velocidad en función del tiempo sabiendo que la velocidad inicial es cero, y calcule la distancia recorrida por el móvil.
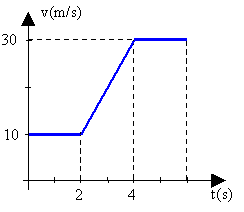
4. La velocidad de un móvil, en movimiento rectilíneo experimenta la variación indicada por el gráfico. Calcular la aceleración media desde \( t = 0 s \) a \( t = 5 s \) y dibujar el gráfico de la aceleración en función del tiempo.
5. El gráfico adjunto, muestra la gráfica de la velocidad en función del tiempo, de un objeto que se mueve en una trayectoria rectilínea. Sabiendo que después del instante \( t = 10 s \), el módulo de la aceleración es el doble que antes, determine el instante de tiempo final en el cual la velocidad es cero.
6. Una pelota se lanza verticalmente hacia arriba, con velocidad inicial \( v_{o} \). Realizar el gráfico de la velocidad en función del tiempo, desde que es lanzada hasta que vuelve a la misma altura donde se soltó.
7. Un cuerpo es lanzado verticalmente hacia arriba con una velocidad de \( 50 \frac {m}{s^2} \). Realice el gráfico de velocidad instantánea en función del tiempo para los primeros \( 10 s \) desde el lanzamiento.
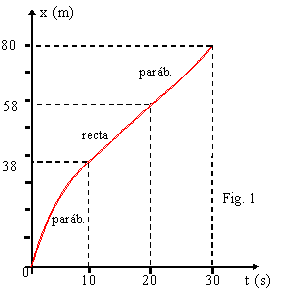
8. En la figura vemos el gráfico de la posición en función del tiempo, para un cuerpo que se mueve en línea recta. Realice la gráfica de la velocidad en función del tiempo.
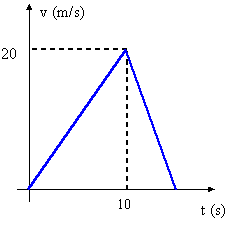
9. Un objeto se mueve sobre una línea recta, de manera que la velocidad varía en función del tiempo, como indica el gráfico. Hallar: el desplazamiento máximo y la aceleración.
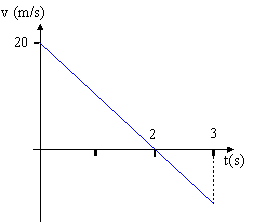
10. El gráfico adjunto representa la velocidad en función del tiempo, de un objeto que se mueve en una trayectoria rectilínea. Sabiendo que a partir de \( t = 10 s \), el módulo de la aceleración, es el doble del que hay entre cero y diez segundos, determine \( t_{f} \).

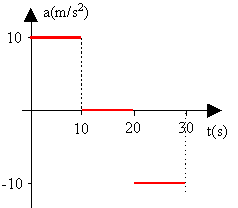
11. La gráfica adjunta, muestra la aceleración de un cuerpo con movimiento rectilíneo en función del tiempo. Sabiendo que la velocidad inicial es cero y parte del reposo, trazar la gráfica de la velocidad en función del tiempo y de la posición en función del tiempo.
12. Un cuerpo se mueve en una trayectoria rectilínea. En el instante \( t_{o} = 0 s\), su velocidad es \( 4,0 \frac {m}{s^2} \) y su aceleración es cero, hasta el instante \( t = 2 s \) en el que se le imprime una aceleración constante de sentido opuesto a la velocidad y módulo \( 5,0 \frac {m}{s^2} \), retornando a la posición que tenía en el instante \( t_{o} \).
Realice el gráfico \( v = f(t) \) entre los instantes \( t_{o} \) y \( t_{f} \).

2. Una esfera se encuentra en el techo de un vagón que parte del reposo con aceleración constante de \( 5,0 \frac {m}{s^2} \) como muestra la figura. Determinar a que distancia se encuentra del vagón, cuando la esfera llega al piso si la altura inicial es de \( 5,0 m \).

3. El gráfico adjunto, corresponde a la aceleración en función del tiempo de un móvil con trayectoria rectilínea. Realizar el gráfico de la velocidad en función del tiempo sabiendo que la velocidad inicial es cero, y calcule la distancia recorrida por el móvil.

4. La velocidad de un móvil, en movimiento rectilíneo experimenta la variación indicada por el gráfico. Calcular la aceleración media desde \( t = 0 s \) a \( t = 5 s \) y dibujar el gráfico de la aceleración en función del tiempo.

5. El gráfico adjunto, muestra la gráfica de la velocidad en función del tiempo, de un objeto que se mueve en una trayectoria rectilínea. Sabiendo que después del instante \( t = 10 s \), el módulo de la aceleración es el doble que antes, determine el instante de tiempo final en el cual la velocidad es cero.

6. Una pelota se lanza verticalmente hacia arriba, con velocidad inicial \( v_{o} \). Realizar el gráfico de la velocidad en función del tiempo, desde que es lanzada hasta que vuelve a la misma altura donde se soltó.
7. Un cuerpo es lanzado verticalmente hacia arriba con una velocidad de \( 50 \frac {m}{s^2} \). Realice el gráfico de velocidad instantánea en función del tiempo para los primeros \( 10 s \) desde el lanzamiento.
8. En la figura vemos el gráfico de la posición en función del tiempo, para un cuerpo que se mueve en línea recta. Realice la gráfica de la velocidad en función del tiempo.

9. Un objeto se mueve sobre una línea recta, de manera que la velocidad varía en función del tiempo, como indica el gráfico. Hallar: el desplazamiento máximo y la aceleración.
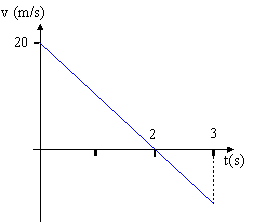
10. El gráfico adjunto representa la velocidad en función del tiempo, de un objeto que se mueve en una trayectoria rectilínea. Sabiendo que a partir de \( t = 10 s \), el módulo de la aceleración, es el doble del que hay entre cero y diez segundos, determine \( t_{f} \).

11. La gráfica adjunta, muestra la aceleración de un cuerpo con movimiento rectilíneo en función del tiempo. Sabiendo que la velocidad inicial es cero y parte del reposo, trazar la gráfica de la velocidad en función del tiempo y de la posición en función del tiempo.

12. Un cuerpo se mueve en una trayectoria rectilínea. En el instante \( t_{o} = 0 s\), su velocidad es \( 4,0 \frac {m}{s^2} \) y su aceleración es cero, hasta el instante \( t = 2 s \) en el que se le imprime una aceleración constante de sentido opuesto a la velocidad y módulo \( 5,0 \frac {m}{s^2} \), retornando a la posición que tenía en el instante \( t_{o} \).
Realice el gráfico \( v = f(t) \) entre los instantes \( t_{o} \) y \( t_{f} \).