|
| Foro Departamento de Matemática Problemas sin resolver Ecuaciones e inecuaciones con valor absoluto |
| Ecuaciones e inecuaciones con valor absoluto |
|
11-04-2013, 10:12 PM
Post: #1
|
|||
|
|||
|
11-04-2013, 10:14 PM
Post: #2
|
|||
|
|||
|
1.
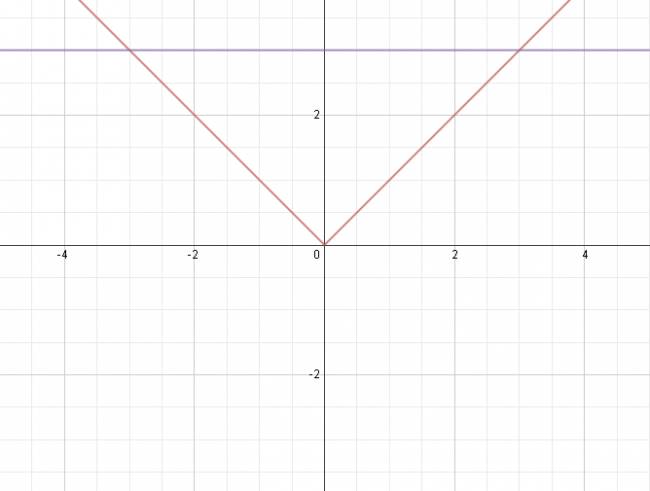
$$ |x| = 3 $$ Por definición de valor absoluto podemos afirmar que: \( x = ± 3 \). Para representar gráficamente debemos considerar a cada miembro como una función: $$ f(x) = |x| $$ $$ g(x) = 3 $$ $$ S = \left\{ -3, +3\right\} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
11-04-2013, 10:18 PM
Post: #3
|
|||
|
|||
|
2.
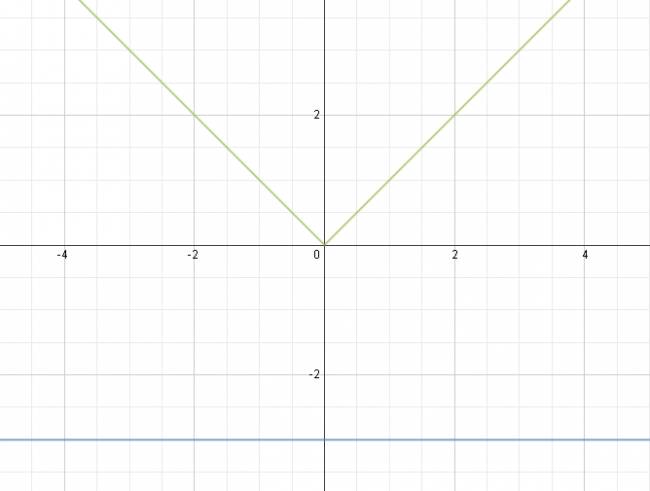
$$ |x| = -3 $$ Por definición de valor absoluto sabemos que esto no es posible, por lo que directamente podemos afirmar que: $$ S = ∅ $$ Volvemos a graficar la expresión por el mismo método que el anterior: $$ f(x) = |x| $$ $$ g(x) = -3 $$ Como vemos, la funciones no se cortan por lo que es correcto afirmar que la solución es vacía, o sea, no existe ningún número que cumpla tal condición. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
11-04-2013, 10:28 PM
Post: #4
|
|||
|
|||
|
3.
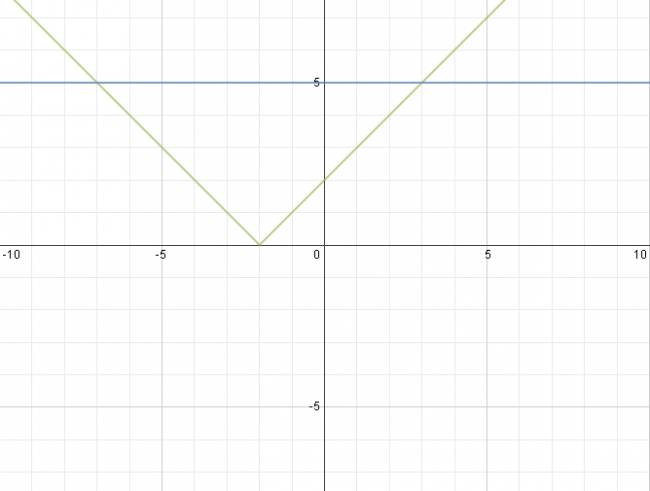
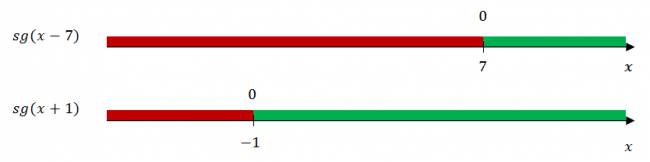
Hasta la anterior pudimos resolver utilizando únicamente la definición, aquí es un poco más difícil, debemos estudiar el dominio. $$ |x+2| = 5 $$ Se estudia únicamente el dominio de la expresión que está en valor absoluto:  El anterior gráfico expresa el comportamiento del signo de la función. Como vemos, antes de -2 es negativo y luego positiva, por lo que vamos a considerar dos tramos, el primero cuando es negativa y el segundo cuando es positiva.  1º Tramo: \( D = (-∞, -2) \) En este tramo vimos que la función es negativa (rojo), por lo que vamos a considerar el opuesto de la expresión: $$ -(x+2) = 5 $$ $$ -x -2 = 5 $$ $$ -x = 7 $$ $$ x = -7 $$ Como vemos, el valor de \( x \) que hallamos está dentro del dominio, ya que es menor que -2, por lo cual podemos afirmar que es solución de la ecuación. 2º Tramo: \( D = (-2, +∞) \) Vimos que luego de -2 la función se comporta de forma positiva, así que vamos a dejar la expresión tal cual está: $$ x+2 = 5 $$ $$ x = 3 $$ Vemos que esta otra raíz también está dentro del dominio, por lo que también es solución de la ecuación. La solución de la ecuación es: $$ S = \left\{ -7,3\right\} $$ Vamos a graficarla para verificar: Les recuerdo que siempre (aunque crean que está bien aplicado el método y bien razonado), lo mejor es verificar de algún modo, ya sea mediante un gráfico o por simplemente valor numérico (sustituir el número en la ecuación, si llegamos a lo mismo de los dos lados, la raíz es correcta ya que verifica la ecuación). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
01-05-2013, 10:02 PM
Post: #5
|
|||
|
|||
|
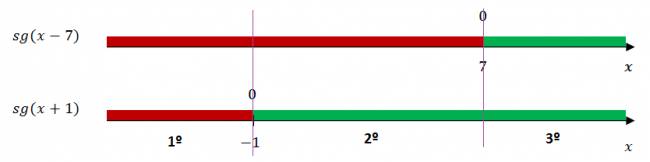
4. Hacemos el estudio del signo de ambas funciones:
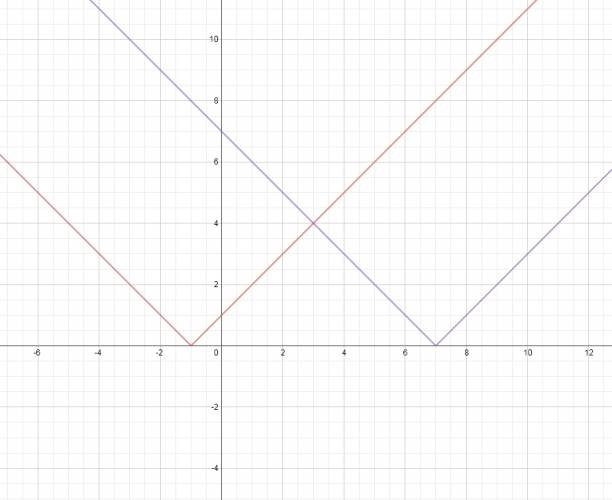
Establecemos los tramos: 1º Tramo: \( D = (-∞, -1) \) $$ -(x+1) = -(x-7) ⇒ -x - 1 = -x + 7 ⇒ S_{1} = ∅ $$ 2º Tramo: \( D = (-1, 7) \) $$ x + 1 = -(x-7) ⇒ x+1=-x+7 ⇒ 2·x = 6 ⇒ x = 3 ⇒ S_{2} = \left\{ 3\right\} $$ 3º Tramo: \( D = (7, +∞) \) $$ x+1=x-7 ⇒ S_{3} = ∅ $$ $$ S = \left\{ 3\right\} $$ Solución gráfica: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-05-2013, 3:58 AM
Post: #6
|
|||
|
|||
|
5.
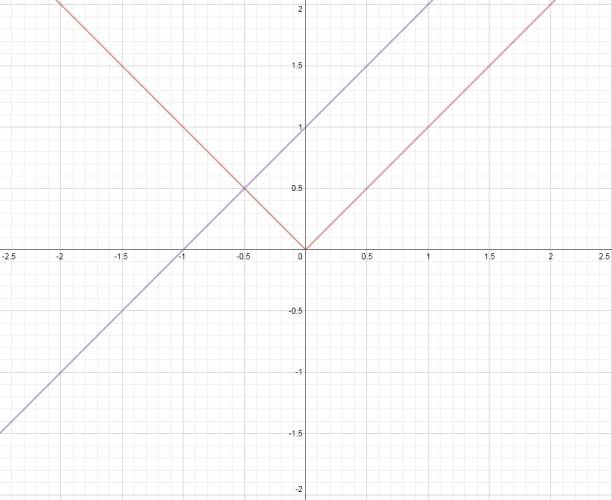
$$ |x| = x + 1 $$ Como siempre: hacemos el estudio del signo de la expresión que está en valor absoluto:  1º Tramo: \( D = (-∞,0) \) Como vemos, en el primer tramo la expresión es negativa (rojo): $$ -x = x + 1 ⇒ -2·x = 1 ⇒ x = - \frac {1}{2} $$ $$ S_{I} = \left\{ - \frac {1}{2} \right\} $$ 2º Tramo: \( D = (0, +∞) \) Como vemos, en el primer tramo la expresión es positiva (verde): $$ x = x + 1 ⇒ ∄x $$ $$ S_{II} = ∅ $$ $$ S = \left\{ - \frac {1}{2} \right\} $$ Solución gráfica: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |