|
| Foro Departamento de Matemática Off-topic Razonamientos aparentemente correctos pero lógicamente incor |
| Razonamientos aparentemente correctos pero lógicamente incor |
|
12-10-2012, 4:27 PM
Post: #1
|
|||
|
|||
|
Razonamientos aparentemente correctos pero lógicamente incorrectos (razonamientos matemáticos falaces)
Hay razonamientos que vemos y a primera vista son correctos, pero a lo que llegan no es cierto. Como puede ser que se llegue a que dos números distintos sean iguales, lo cual no es correcto. No es lo mismo tener dos manzanas a tener una. Estos razonamientos andan por toda la red y desconciertan a mucha gente. Intentaré hacer un compilado de ellos y ver cuales son los errores lógicos. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-10-2012, 4:27 PM
Post: #2
|
|||
|
|||
|
Razonamiento:
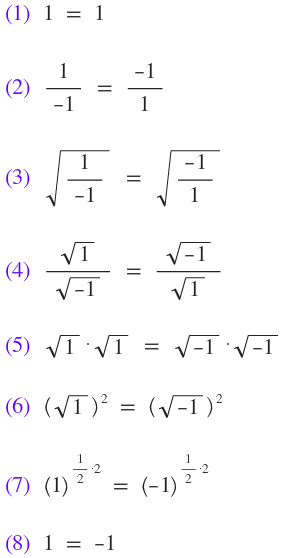 Error lógico: Una de las propiedades que se utiliza en el razonamiento es la siguiente:  Como se puede ver, una de las condiciones es que tanto a como b sean números naturales (positivos) para que se cumple esta propiedad. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-10-2012, 7:50 PM
Post: #3
|
|||
|
|||
|
Razonamiento:
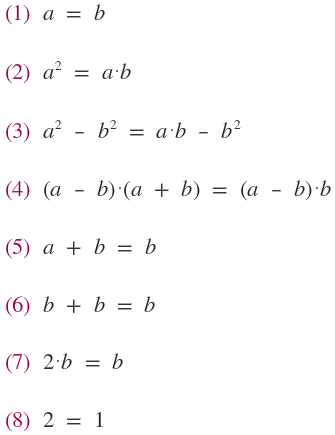 Error lógico: Ver en el renglón 4: a ambos miembros de la igualdad está el factor (a-b), se puede razonar lo mismo de dos formas: 1. Se utilizan propiedades de forma errónea: Por la propiedad cancelativa de la multiplicación podemos quitar un mismo factor que se repite en ambos lados del signo de igualdad siempre y cuando no sea cero. Al principio habíamos dicho que: a = b, supongamos: a = b = 5, y lo que nos dice es que ese mismo número se resta, o sea, 5-5=0, y estaríamos cancelando un cero, lo cual la propiedad no permite. 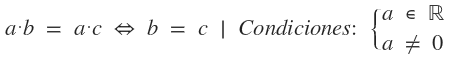 2. Se despeja de forma errónea: Decimos que: a = b, y supongamos un número cualquier, por ejemplo 5: (a-b) = (5-5) = 0, y cuando pasamos a dividir el factor al otro lado del signo de igual lo que hacemos es dividir por cero, lo cual no es posible.  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
17-10-2012, 8:58 AM
Post: #4
|
|||
|
|||
|
Razonamiento:
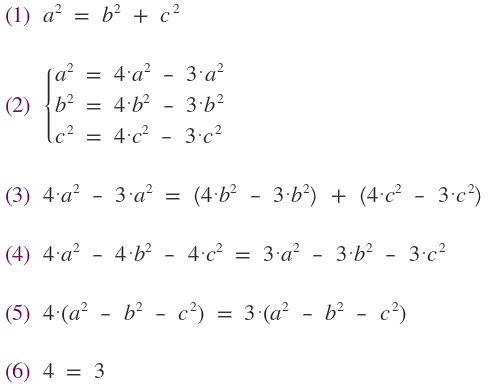 Error lógico: Está cancelando un cero o bien dividiendo por cero, lo cual no es posible. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-03-2013, 10:43 PM
Post: #5
|
|||
|
|||
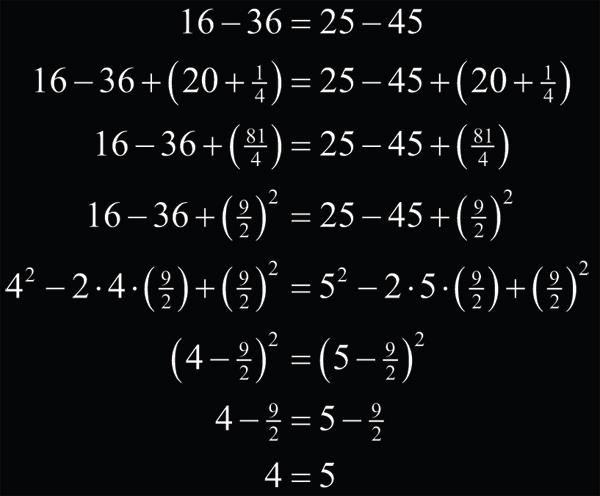 En el momento que radicó ambos miembros, tendría que haber utilizado valor absoluto: $$ \left ( 4 - \frac {9}{2} \right )^2 = \left ( 5 - \frac {9}{2} \right )^2 $$ $$ | 4 - \frac {9}{2} | = | 5 - \frac {9}{2} | $$ De lo contrario, no es cierta tal igualdad y se puede deducir cualquier cosa ilógica a partir de ello, como fue el caso del ejemplo. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |







