|
| Foro Departamento de Física Teóricos Deducción de las fórmulas de movimiento variado |
| Deducción de las fórmulas de movimiento variado |
|
16-12-2012, 4:25 PM
Post: #1
|
|||
|
|||
|
Deducción de las fórmulas de movimiento variado
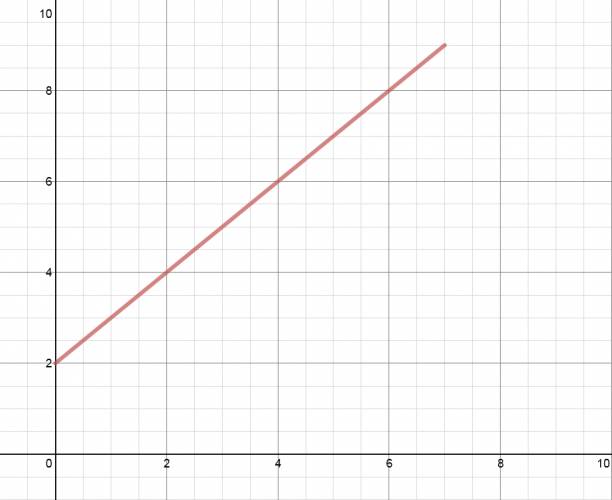
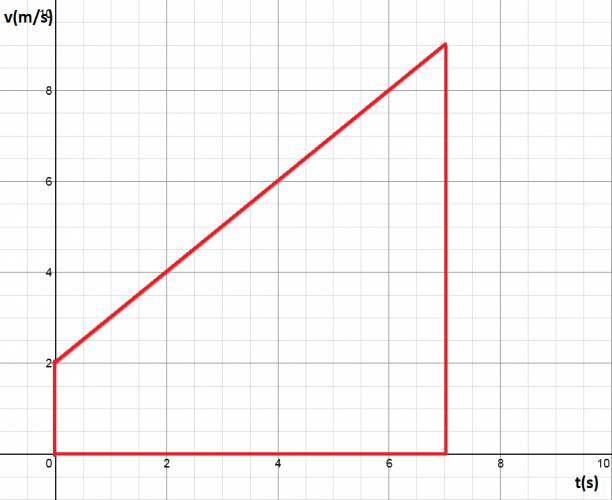
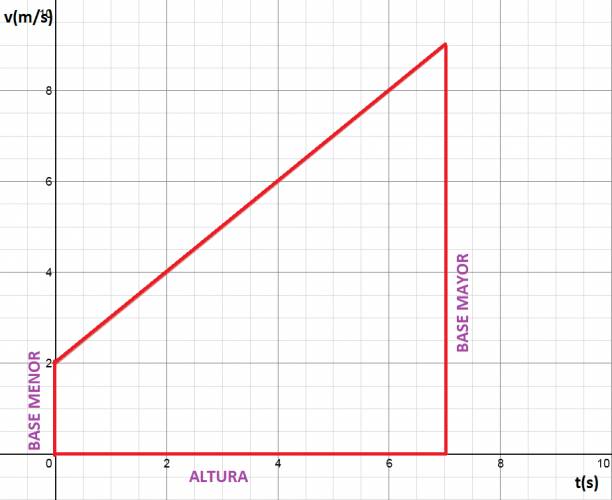
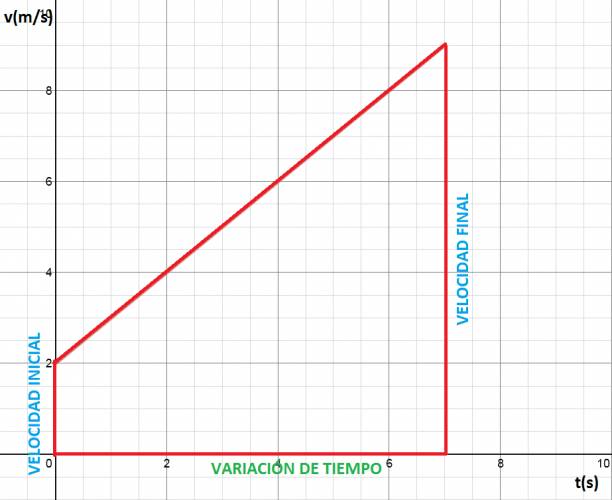
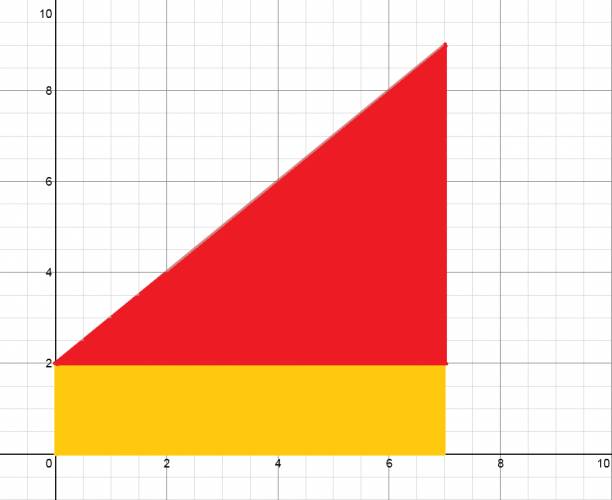
PRIMER FÓRMULA: Partimos de la siguiente premisa: "el área bajo la gráfica \( v(t) \) nos da el desplazamiento". Un ejemplo de gráfica de \( v(t) \) sería: Ahora, vamos a destacar la parte debajo la gráfica: Lo cual forma un trapecio, y su área es el desplazamiento. El área del trapecio se calcula como: $$ á trapecio = \frac {(basemayor+basemenor)·altura}{2} $$ Lo que conocemos es esto: Ahora simplemente sustituimos en la fórmula del área del trapecio: $$ á trapecio = \Delta x = \frac {(v_{f}+v_{i})· \Delta t}{2} $$ SEGUNDA FÓRMULA: Partimos de la fórmula anterior. Sabemos, por definición de aceleración, que se calcula como: $$ a = \frac {v_{f} - v_{i}}{\Delta t} \Rightarrow \Delta t = \frac {v_{f} - v_{i}}{a} $$ Ahora sustituimos \( \Delta t \) en la fórmula ya deducida: $$ \Delta x = \frac {(v_{f}+v_{i})· \Delta t}{2} \Rightarrow \Delta x = \frac {(v_{f}+v_{i})· \frac {v_{f} - v_{i}}{a}}{2} \Rightarrow \Delta x = \frac {v_{f}^2 - v_{i^2}}{2·a} $$ TERCERA FÓRMULA: Partimos de la gráfica, pero en vez de tomar el trapecio, vamos a tomar el área del rectángulo y el área del triángulo. $$ á rectángulo = b·h \Rightarrow á rectángulo = \Delta t · v_{i} $$ $$ á triángulo = \frac {b·h}{2} \Rightarrow á triángulo = \frac {\Delta t · (v_{f} - v_{i})}{2} $$ Pero, despejamos de la fórmula primaria de aceleración: $$ v_{f} - v_{i} = a · \Delta t $$ Ahora sustituyendo, nos queda que: $$ á triángulo = \frac {b·h}{2} \Rightarrow á triángulo = \frac {\Delta t · (a· \Delta t)}{2} \Rightarrow á triángulo = \frac {a· \Delta t^2}{2} $$ $$ á gráfica = á rectángulo + á triángulo \Rightarrow \Delta x = v_{i}· \Delta t + \frac {a· \Delta t^2}{2} $$ Absolutamente todo problema de movimiento variado se puede resolver con estas fórmulas: $$ a = \frac {\Delta v}{ \Delta t} $$ $$ \Delta x = \frac{(v_{f} + v_{i})· \Delta t}{2} $$ $$ \Delta x = \frac{v_{f}^2 - v_{i}^2}{2·a} $$ $$ x_{f} = x_{i} + v_{o}· \Delta t + \frac {a· \Delta t^2}{2} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |