16-12-2012, 4:25 PM
Deducción de las fórmulas de movimiento variado
PRIMER FÓRMULA:
Partimos de la siguiente premisa: "el área bajo la gráfica \( v(t) \) nos da el desplazamiento".
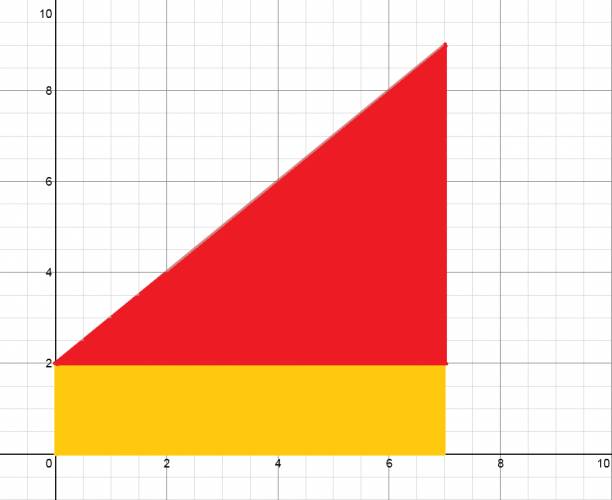
Un ejemplo de gráfica de \( v(t) \) sería:
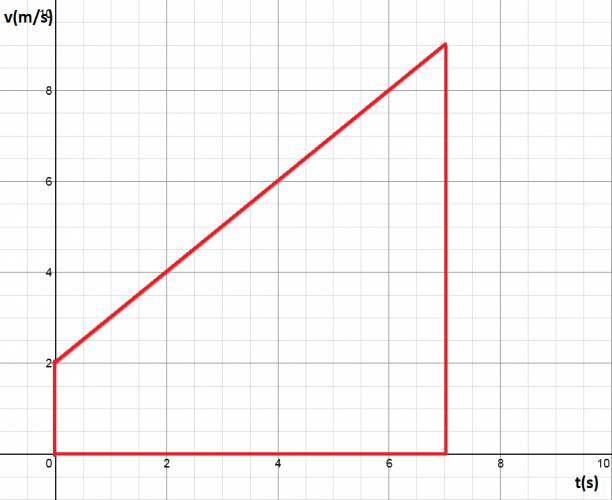
Ahora, vamos a destacar la parte debajo la gráfica:
Lo cual forma un trapecio, y su área es el desplazamiento. El área del trapecio se calcula como:
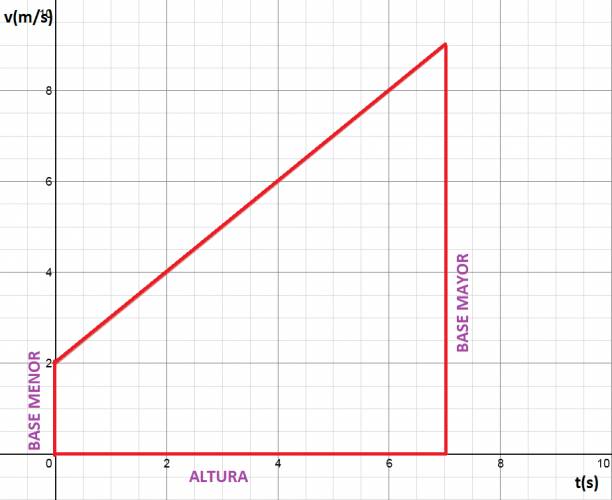
$$ á trapecio = \frac {(basemayor+basemenor)·altura}{2} $$
Lo que conocemos es esto:
Ahora simplemente sustituimos en la fórmula del área del trapecio:
$$ á trapecio = \Delta x = \frac {(v_{f}+v_{i})· \Delta t}{2} $$
SEGUNDA FÓRMULA:
Partimos de la fórmula anterior. Sabemos, por definición de aceleración, que se calcula como:
$$ a = \frac {v_{f} - v_{i}}{\Delta t} \Rightarrow \Delta t = \frac {v_{f} - v_{i}}{a} $$
Ahora sustituimos \( \Delta t \) en la fórmula ya deducida:
$$ \Delta x = \frac {(v_{f}+v_{i})· \Delta t}{2} \Rightarrow \Delta x = \frac {(v_{f}+v_{i})· \frac {v_{f} - v_{i}}{a}}{2} \Rightarrow \Delta x = \frac {v_{f}^2 - v_{i^2}}{2·a} $$
TERCERA FÓRMULA:
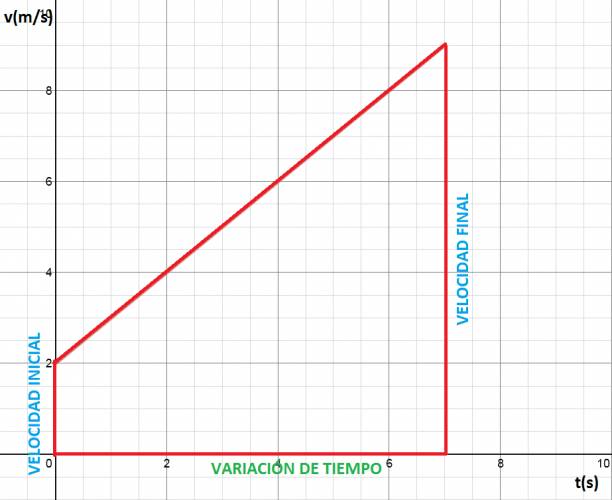
Partimos de la gráfica, pero en vez de tomar el trapecio, vamos a tomar el área del rectángulo y el área del triángulo.
$$ á rectángulo = b·h \Rightarrow á rectángulo = \Delta t · v_{i} $$
$$ á triángulo = \frac {b·h}{2} \Rightarrow á triángulo = \frac {\Delta t · (v_{f} - v_{i})}{2} $$
Pero, despejamos de la fórmula primaria de aceleración:
$$ v_{f} - v_{i} = a · \Delta t $$
Ahora sustituyendo, nos queda que:
$$ á triángulo = \frac {b·h}{2} \Rightarrow á triángulo = \frac {\Delta t · (a· \Delta t)}{2} \Rightarrow á triángulo = \frac {a· \Delta t^2}{2} $$
$$ á gráfica = á rectángulo + á triángulo \Rightarrow \Delta x = v_{i}· \Delta t + \frac {a· \Delta t^2}{2} $$
Absolutamente todo problema de movimiento variado se puede resolver con estas fórmulas:
PRIMER FÓRMULA:
Partimos de la siguiente premisa: "el área bajo la gráfica \( v(t) \) nos da el desplazamiento".
Un ejemplo de gráfica de \( v(t) \) sería:
Ahora, vamos a destacar la parte debajo la gráfica:
Lo cual forma un trapecio, y su área es el desplazamiento. El área del trapecio se calcula como:
$$ á trapecio = \frac {(basemayor+basemenor)·altura}{2} $$
Lo que conocemos es esto:
Ahora simplemente sustituimos en la fórmula del área del trapecio:
$$ á trapecio = \Delta x = \frac {(v_{f}+v_{i})· \Delta t}{2} $$
SEGUNDA FÓRMULA:
Partimos de la fórmula anterior. Sabemos, por definición de aceleración, que se calcula como:
$$ a = \frac {v_{f} - v_{i}}{\Delta t} \Rightarrow \Delta t = \frac {v_{f} - v_{i}}{a} $$
Ahora sustituimos \( \Delta t \) en la fórmula ya deducida:
$$ \Delta x = \frac {(v_{f}+v_{i})· \Delta t}{2} \Rightarrow \Delta x = \frac {(v_{f}+v_{i})· \frac {v_{f} - v_{i}}{a}}{2} \Rightarrow \Delta x = \frac {v_{f}^2 - v_{i^2}}{2·a} $$
TERCERA FÓRMULA:
Partimos de la gráfica, pero en vez de tomar el trapecio, vamos a tomar el área del rectángulo y el área del triángulo.
$$ á rectángulo = b·h \Rightarrow á rectángulo = \Delta t · v_{i} $$
$$ á triángulo = \frac {b·h}{2} \Rightarrow á triángulo = \frac {\Delta t · (v_{f} - v_{i})}{2} $$
Pero, despejamos de la fórmula primaria de aceleración:
$$ v_{f} - v_{i} = a · \Delta t $$
Ahora sustituyendo, nos queda que:
$$ á triángulo = \frac {b·h}{2} \Rightarrow á triángulo = \frac {\Delta t · (a· \Delta t)}{2} \Rightarrow á triángulo = \frac {a· \Delta t^2}{2} $$
$$ á gráfica = á rectángulo + á triángulo \Rightarrow \Delta x = v_{i}· \Delta t + \frac {a· \Delta t^2}{2} $$
Absolutamente todo problema de movimiento variado se puede resolver con estas fórmulas:
$$ a = \frac {\Delta v}{ \Delta t} $$
$$ \Delta x = \frac{(v_{f} + v_{i})· \Delta t}{2} $$
$$ \Delta x = \frac{v_{f}^2 - v_{i}^2}{2·a} $$
$$ x_{f} = x_{i} + v_{o}· \Delta t + \frac {a· \Delta t^2}{2} $$
$$ \Delta x = \frac{(v_{f} + v_{i})· \Delta t}{2} $$
$$ \Delta x = \frac{v_{f}^2 - v_{i}^2}{2·a} $$
$$ x_{f} = x_{i} + v_{o}· \Delta t + \frac {a· \Delta t^2}{2} $$