|
| Foro Departamento de Física Teóricos Ley de gravitación universal |
| Ley de gravitación universal |
|
09-11-2012, 10:26 PM
Post: #1
|
|||
|
|||
|
Ley de gravitación universal
Atribuida a Isaac Newton, aunque se sospecha que éste mandó asesinar a su verdadero descubridor, Robert Hooke.  Definición: La fuerza de atracción de dos cuerpos cualesquiera es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. 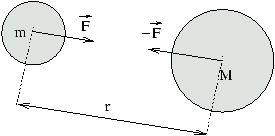 Expresión matemática: $$ F = \frac {G·m_{1}·m_{2}}{d^2} $$ Siendo G la constante de gravitación universal: $$ G = 6,67 · 10^{-11} \frac {N·m^2}{C^2} $$ Que fue determinada por primera vez por Henry Cavendish en 1798. Explicación: Por la tercera ley de Newton sabemos que las fuerzas atractivas de dos cuerpos son iguales y opuestas (mismo módulo, misma dirección, distinto punto de aplicación, y sentido opuesto). Dos cuerpos cualesquiera, por el simple hecho de existir y poseer masa se ejercen mutuamente una fuerza (que es igual y opuesta), el módulo de esta fuerza se puede calcular a través de la anterior fórmula. Un concepto muy importante que introdujo Newton fue que la masa atrae masa:  Relación de proporcionalidad: $$ \left . \begin{matrix} F \propto m_{1}·m_{2} \\ F \propto \frac {1}{d^2} \end{matrix} \right \} ⇒ F \propto \frac {m_{1}·m_{2}}{d^2} $$ · \( F \alpha m_{1}·m_{2} \): léase que el producto de las masas es directamente proporcional a la fuerza, esto significa que si una de las masas aumenta al doble, también lo hará la fuerza atractiva. · \( F \alpha \frac {1}{d^2} \): léase que la distancia al cuadrado es inversamente proporcional a la fuerza, esto significa que si la fuerza aumenta al doble, la fuerza disminuirá a la mitad. Peso no es lo mismo que masa: El peso es una magnitud vectorial, mientas que la masa es una magnitud escalar. El peso se mide en N (newton), la masa se mide en kg (kilogramo). La masa es la cantidad de materia que posee un cuerpo. El peso es la fuerza con la que el planeta Tierra atrae a dicha masa. Para conocer el peso de un cuerpo, se debe multiplicar la masa del cuerpo la aceleración gravitatoria (g): $$ P = m · g $$ Si decimos que un cuerpo tiene 10 kg de masa, entonces su peso será: $$ P = m · g $$ $$ P = 10 kg · 9,8 \frac {m}{s^2} $$ $$ P = 98 N $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
04-12-2012, 6:19 PM
Post: #2
|
|||
|
|||
|
Deducción de la fórmula de peso:
Partimos de la ley de gravitación universal: $$ F = \frac{G·m_{1}·m_{2}}{d^2} $$ Que nos dice que la fuerza que se ejercen dos cuerpos se puede calcular con la fórmula expuesta arriba. El peso de un cuerpo es la fuerza con la que el planeta Tierra atrae hacia su centro a la masa de ese cuerpo, esto nos dice que el peso se calcula con la fórmula de gravitación universal. Siempre que calculamos el peso de un cuerpo, hay algo que no varía: la masa y el radio terrestre, lo único que cambia es la masa del cuerpo que se quiere conocer su peso. Por lo que, de toda la fórmula anterior, lo simplificamos y llamamos a toda la parte de: $$ g = \frac{G·m_{T}}{r_{T}^2} $$ Como vemos, lo único que falta es multiplicar por otro masa y obtenemos el valor del peso de un cuerpo: $$ P = m·g = m · \frac{G·m_{T}}{r_{T}^2} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
04-12-2012, 6:21 PM
Post: #3
|
|||
|
|||
|
Aceleración gravitatoria en los distintos planetas del sistema solar y de la luna terrestre:
Planetas del sistema solar: Mercurio: 3,70 \( \frac {m}{s^2} \) Venus: 8,87 \( \frac {m}{s^2} \) Tierra: 9,80 \( \frac {m}{s^2} \) Marte: 3,71 \( \frac {m}{s^2} \) Júpiter: 23,12 \( \frac {m}{s^2} \) Saturno: 8,96 \( \frac {m}{s^2} \) Urano: 8,69 \( \frac {m}{s^2} \) Neptuno: 11 \( \frac {m}{s^2} \) Plutón: 0,81 \( \frac {m}{s^2} \) Luna: 1,62 \( \frac {m}{s^2} \) ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |







