09-11-2012, 10:26 PM
Ley de gravitación universal
Atribuida a Isaac Newton, aunque se sospecha que éste mandó asesinar a su verdadero descubridor, Robert Hooke.

Definición:
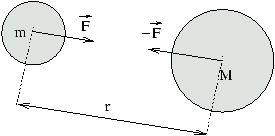
La fuerza de atracción de dos cuerpos cualesquiera es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.
Expresión matemática:
$$ F = \frac {G·m_{1}·m_{2}}{d^2} $$
Siendo G la constante de gravitación universal:
$$ G = 6,67 · 10^{-11} \frac {N·m^2}{C^2} $$
Que fue determinada por primera vez por Henry Cavendish en 1798.
Explicación:
Por la tercera ley de Newton sabemos que las fuerzas atractivas de dos cuerpos son iguales y opuestas (mismo módulo, misma dirección, distinto punto de aplicación, y sentido opuesto). Dos cuerpos cualesquiera, por el simple hecho de existir y poseer masa se ejercen mutuamente una fuerza (que es igual y opuesta), el módulo de esta fuerza se puede calcular a través de la anterior fórmula.
Un concepto muy importante que introdujo Newton fue que la masa atrae masa:

Relación de proporcionalidad:
$$ \left .
\begin{matrix}
F \propto m_{1}·m_{2} \\
F \propto \frac {1}{d^2}
\end{matrix}
\right \} ⇒ F \propto \frac {m_{1}·m_{2}}{d^2} $$
· \( F \alpha m_{1}·m_{2} \): léase que el producto de las masas es directamente proporcional a la fuerza, esto significa que si una de las masas aumenta al doble, también lo hará la fuerza atractiva.
· \( F \alpha \frac {1}{d^2} \): léase que la distancia al cuadrado es inversamente proporcional a la fuerza, esto significa que si la fuerza aumenta al doble, la fuerza disminuirá a la mitad.
Peso no es lo mismo que masa:
El peso es una magnitud vectorial, mientas que la masa es una magnitud escalar. El peso se mide en N (newton), la masa se mide en kg (kilogramo).
La masa es la cantidad de materia que posee un cuerpo. El peso es la fuerza con la que el planeta Tierra atrae a dicha masa. Para conocer el peso de un cuerpo, se debe multiplicar la masa del cuerpo la aceleración gravitatoria (g):
$$ P = m · g $$
Si decimos que un cuerpo tiene 10 kg de masa, entonces su peso será:
$$ P = m · g $$
$$ P = 10 kg · 9,8 \frac {m}{s^2} $$
$$ P = 98 N $$
Atribuida a Isaac Newton, aunque se sospecha que éste mandó asesinar a su verdadero descubridor, Robert Hooke.

Definición:
La fuerza de atracción de dos cuerpos cualesquiera es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa.

Expresión matemática:
$$ F = \frac {G·m_{1}·m_{2}}{d^2} $$
Siendo G la constante de gravitación universal:
$$ G = 6,67 · 10^{-11} \frac {N·m^2}{C^2} $$
Que fue determinada por primera vez por Henry Cavendish en 1798.
Explicación:
Por la tercera ley de Newton sabemos que las fuerzas atractivas de dos cuerpos son iguales y opuestas (mismo módulo, misma dirección, distinto punto de aplicación, y sentido opuesto). Dos cuerpos cualesquiera, por el simple hecho de existir y poseer masa se ejercen mutuamente una fuerza (que es igual y opuesta), el módulo de esta fuerza se puede calcular a través de la anterior fórmula.
Un concepto muy importante que introdujo Newton fue que la masa atrae masa:

Relación de proporcionalidad:
$$ \left .
\begin{matrix}
F \propto m_{1}·m_{2} \\
F \propto \frac {1}{d^2}
\end{matrix}
\right \} ⇒ F \propto \frac {m_{1}·m_{2}}{d^2} $$
· \( F \alpha m_{1}·m_{2} \): léase que el producto de las masas es directamente proporcional a la fuerza, esto significa que si una de las masas aumenta al doble, también lo hará la fuerza atractiva.
· \( F \alpha \frac {1}{d^2} \): léase que la distancia al cuadrado es inversamente proporcional a la fuerza, esto significa que si la fuerza aumenta al doble, la fuerza disminuirá a la mitad.
Peso no es lo mismo que masa:
El peso es una magnitud vectorial, mientas que la masa es una magnitud escalar. El peso se mide en N (newton), la masa se mide en kg (kilogramo).
La masa es la cantidad de materia que posee un cuerpo. El peso es la fuerza con la que el planeta Tierra atrae a dicha masa. Para conocer el peso de un cuerpo, se debe multiplicar la masa del cuerpo la aceleración gravitatoria (g):
$$ P = m · g $$
Si decimos que un cuerpo tiene 10 kg de masa, entonces su peso será:
$$ P = m · g $$
$$ P = 10 kg · 9,8 \frac {m}{s^2} $$
$$ P = 98 N $$