|
| Foro Departamento de Matemática Teóricos Geometría analítica en el plano: la hipérbola |
| Geometría analítica en el plano: la hipérbola |
|
24-10-2013, 6:58 PM
Post: #1
|
|||
|
|||
|
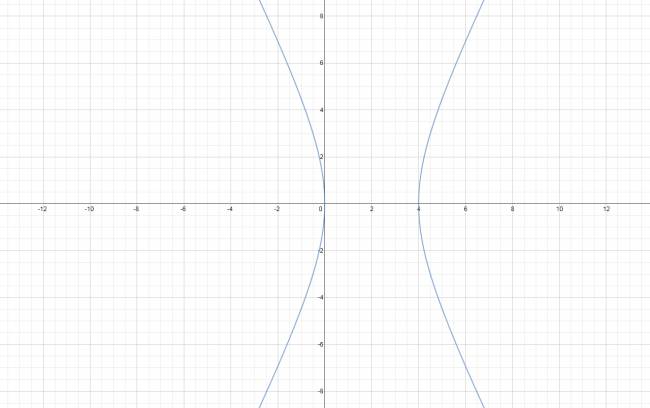
Hipérbola
Una hipérbola es una figura cónica. Elementos de una hipérbola: Ecuación de la hipérbola: · Toda hipérbola de eje focal paralelo a \( O \vec x \) se puede expresar de la forma reducida: $$ \frac {(x-h)^2}{a^2} - \frac {(y-k)^2}{b^2} = 1 $$ · Toda hipérbola de eje focal paralelo a \( O \vec y \) se puede expresar de la forma reducida: $$ \frac {(y-k)^2}{a^2} - \frac {(h-x)^2}{b^2} = 1 $$ Donde su centro es \( O'(h,k) \). La forma desarrollada de una hipérbola es: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \) que también es la ecuación de cualquier cónica, por lo cual, no es recomendable trabajar con ella en forma desarrollada. La hipérbola es la única de las cuatro figuras cónicas que presenta asíntotas; recordemos que toda hipérbola presenta dos asíntotas. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
24-10-2013, 6:59 PM
Post: #2
|
|||
|
|||
|
· Determinar el centro de una hipérbola conociendo su ecuación en forma desarrollada:
La ecuación de una hipérbola desarrollada es de la forma: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \). La raíz de la derivada parcial con respecto a la variable \( x \), será la abscisa del centro de la hipérbola; mientras que la raíz de la derivada parcial con respecto a la variable \( y \), será la ordenada del centro de la hipérbola. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
20-11-2013, 2:14 AM
Post: #3
|
|||
|
|||
|
Hipérbola equilátera
Definición: Una hipérbola es equilátera si y sólo si cumple que \( a = b \). A causa de su definición, cumplirá que sus dos asíntotas son perpendiculares entre sí. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
20-11-2013, 2:17 AM
Post: #4
|
|||
|
|||
|
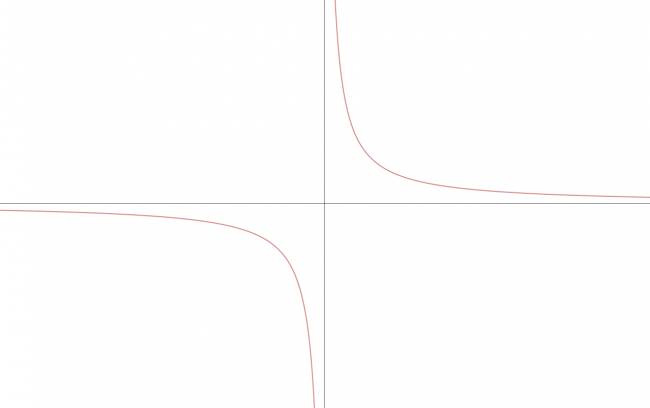
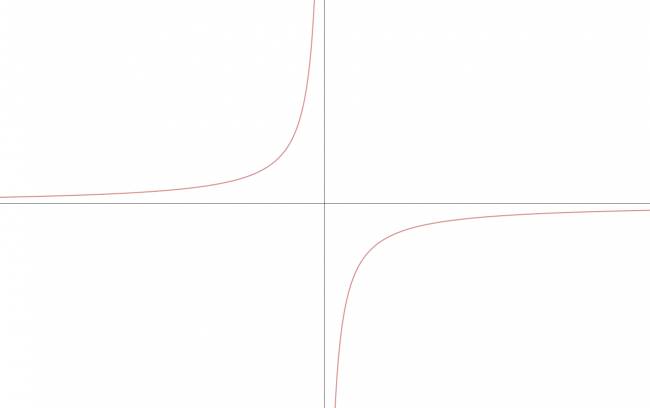
Hipérbola equilátera cuyas asíntotas son los ejes coordenados
La ecuación de cualquier hipérbola equilátera cuyas asíntotas sean los ejes coordenados se puede expresar de la siguiente forma: $$ x·y = k, k∈ℝ^{*} $$ · Primer caso: hipérbola equilátera cuyas asíntotas son ejes coordenados, 1er y 3er cuadrante. Es el caso en que \( k > 0 \). En este caso: \( k = \frac {a^2}{2} \) · Segundo caso: hipérbola equilátera cuyas asíntotas son ejes coordenados, 2do y 4to cuadrante. Es el caso en que \( k < 0 \). En este caso: \( k = -\frac {a^2}{2} \) ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |