24-10-2013, 6:58 PM
Hipérbola
Una hipérbola es una figura cónica.
Elementos de una hipérbola:
Ecuación de la hipérbola:
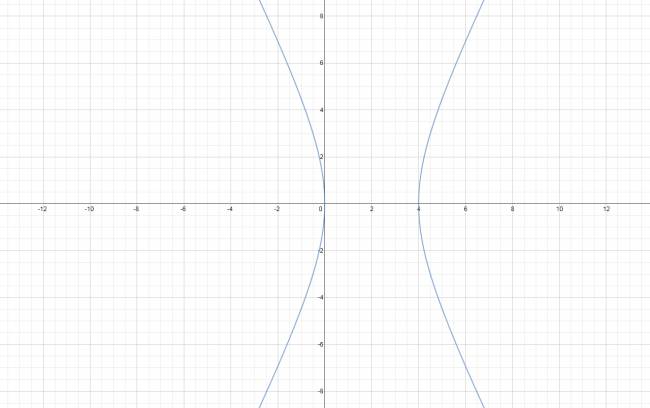
· Toda hipérbola de eje focal paralelo a \( O \vec x \) se puede expresar de la forma reducida:
$$ \frac {(x-h)^2}{a^2} - \frac {(y-k)^2}{b^2} = 1 $$
· Toda hipérbola de eje focal paralelo a \( O \vec y \) se puede expresar de la forma reducida:
$$ \frac {(y-k)^2}{a^2} - \frac {(h-x)^2}{b^2} = 1 $$
Donde su centro es \( O'(h,k) \).
La forma desarrollada de una hipérbola es: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \) que también es la ecuación de cualquier cónica, por lo cual, no es recomendable trabajar con ella en forma desarrollada.
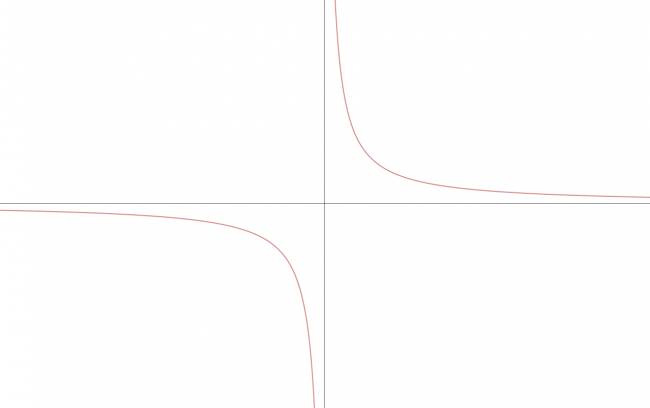
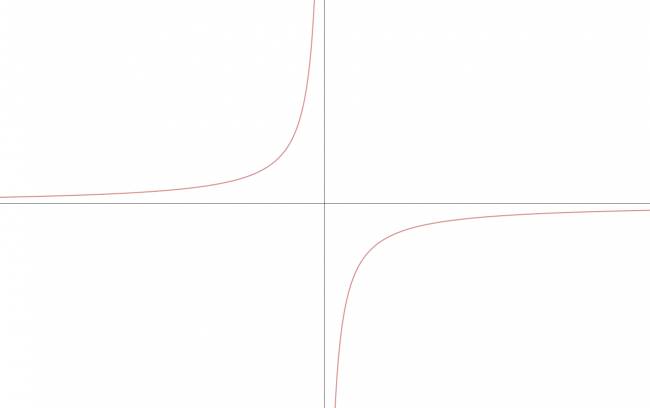
La hipérbola es la única de las cuatro figuras cónicas que presenta asíntotas; recordemos que toda hipérbola presenta dos asíntotas.
Una hipérbola es una figura cónica.
Elementos de una hipérbola:
Ecuación de la hipérbola:
· Toda hipérbola de eje focal paralelo a \( O \vec x \) se puede expresar de la forma reducida:
$$ \frac {(x-h)^2}{a^2} - \frac {(y-k)^2}{b^2} = 1 $$
· Toda hipérbola de eje focal paralelo a \( O \vec y \) se puede expresar de la forma reducida:
$$ \frac {(y-k)^2}{a^2} - \frac {(h-x)^2}{b^2} = 1 $$
Donde su centro es \( O'(h,k) \).
La forma desarrollada de una hipérbola es: \( A·x^2 + B·x·y + C·y^2 + D·x + E·y + F = 0 \) que también es la ecuación de cualquier cónica, por lo cual, no es recomendable trabajar con ella en forma desarrollada.
La hipérbola es la única de las cuatro figuras cónicas que presenta asíntotas; recordemos que toda hipérbola presenta dos asíntotas.