|
| Foro Departamento de Matemática Teóricos Función exponencial |
| Función exponencial |
|
15-09-2013, 9:41 PM
Post: #1
|
|||
|
|||
|
Función exponencial
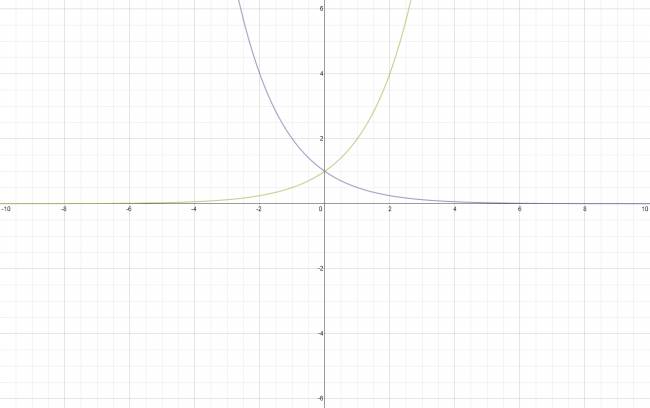
Las funciones exponenciales son del tipo: $$ f(x) = a^{x} $$ Condición: \( a∈ℝ^{+} \) \( a ≠ 1 \) O sea, es una constante elevada a una función. Para estudiar esta función, vamos a dividirla en dos grandes categorías, esto se debe a que sus gráficos son distintos. Distinción: a. \( 0 < a < 1 \) b. \( 1 < a \) ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
15-09-2013, 9:50 PM
Post: #2
|
|||
|
|||
|
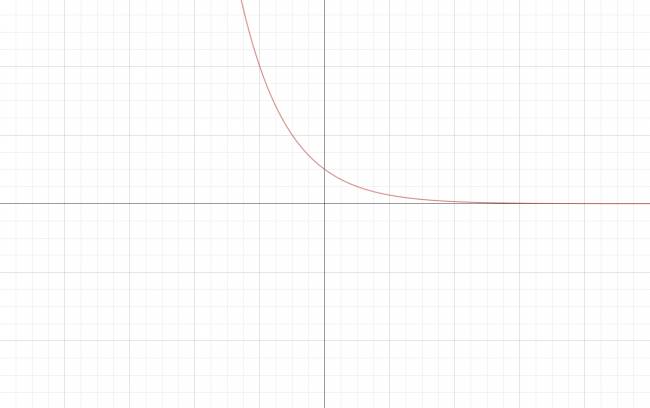
Función exponencial de base \( 0 < a < 1 \):
Características: · Es una función creciente. · No tiene raíces: \( S = ∅ \) · Su ordenada en el origen es \( [0,1] \). · Su dominio es: \( D = ℝ \). · Su codominio es: \( C = ℝ^{+} \). Gráfico: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
15-09-2013, 9:51 PM
Post: #3
|
|||
|
|||
|
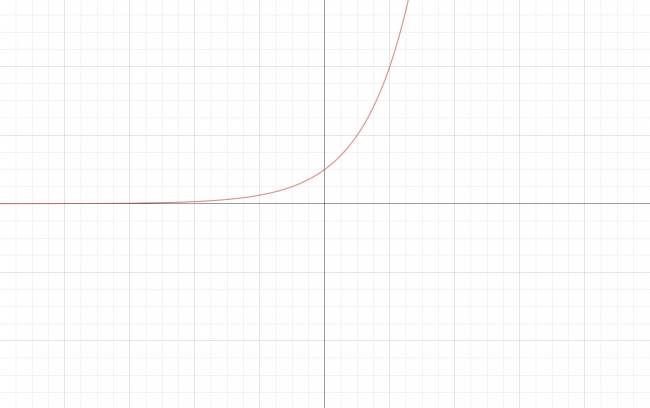
Función exponencial de base \( a > 1 \):
Características: · Es una función decreciente. · No tiene raíces: \( S = ∅ \) · Su ordenada en el origen es \( [0,1] \). · Su dominio es: \( D = ℝ \). · Su codominio es: \( C = ℝ^{+} \). Gráfico: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
22-09-2013, 4:09 AM
Post: #4
|
|||
|
|||
|
Resolución de una ecuación exponencial:
· 1er tipo: si son de igual base o se pueden llevar a igual base sin aplicar logaritmos: $$ a^{p(x)} = a^{q(x)} ⇒ p(x) = q(x) $$ Se resuelve la ecuación a la que se ha llegado, su conjunto solución es el mismo del de la ecuación exponencial original. · 2do tipo: si son de distinta base y no se pueden llevar a la misma base sin aplicar logaritmos: $$ a^{p(x)} = b^{q(x)} ⇒ [p(x)]·\ln(a) = [q(x)]·\ln(b) $$ Se aplican las distributivas necesarias (dependiendo de la función) y se lleva todo a un mismo miembro, luego, se ordenada en la variable y resuelve la ecuación, su conjunto solución es el mismo del de la ecuación exponencial original. · 3er tipo: si la ecuación exponencial es más compleja, entiéndase, que tiene más términos: $$ p(x) + a^{q(x)} = 0 $$ Se aplica un cambio de variable conveniente. · 4to caso: si se trata de una suma de términos (progresión geométrica): $$ a_{1} + a_{2} + a_{3} + ... + a^{x} = b $$ Se puede resolver fácilmente a través de la siguiente fórmula (deducida a partir de la de progresión geométrica): $$ x = \log_{a} \left ( \frac {b·(a_{3}-a_{2})+a_{1}·a_{2}}{a_{3}} \right ) $$ · 5to caso: si es sencilla, del tipo: $$ a^{x} = b $$ Se aplica la definición de logaritmo: $$ x = \log_{a} (b) $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |