Universo Científico :: Función exponencial

Página 1 de 1
1

Función exponencial

Las funciones exponenciales son del tipo:
$$ f(x) = a^{x} $$

Condición:
$ a∈ℝ^{+} $
$ a ≠ 1 $

O sea, es una constante elevada a una función.

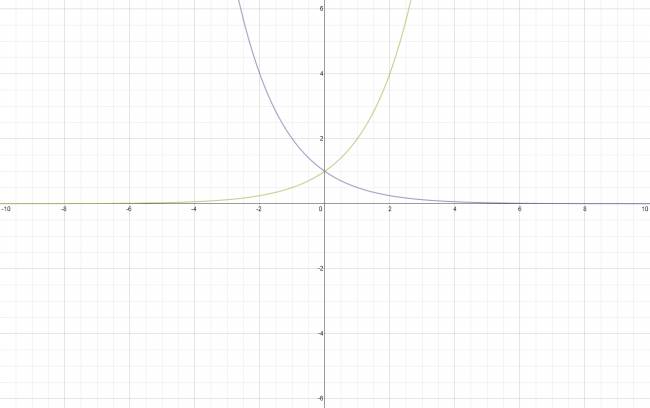
Para estudiar esta función, vamos a dividirla en dos grandes categorías, esto se debe a que sus gráficos son distintos.

Distinción:
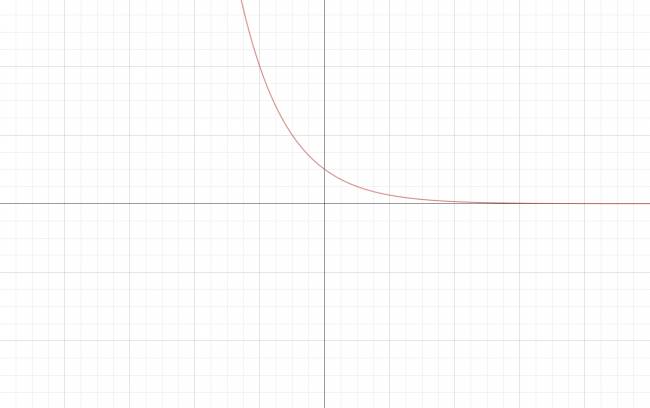
a. $ 0 < a < 1 $
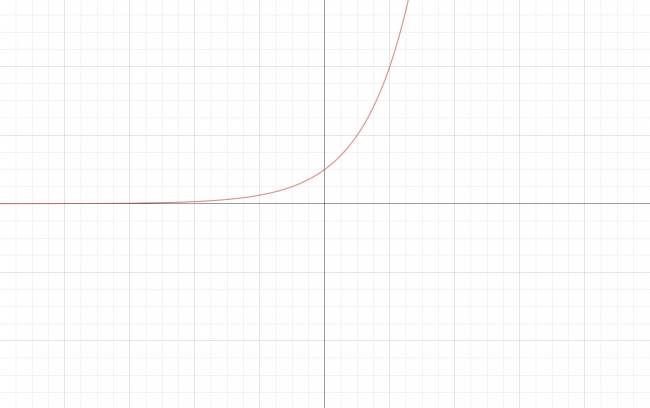
b. $ 1 < a $

Cita

$$ a(x) = 2^{x} $$
$$ b(x) = \left ( \frac {1}{2} \right )^{x} $$

Función exponencial de base $ 0 < a < 1 $:

Características:
· Es una función creciente.
· No tiene raíces: $ S = ∅ $
· Su ordenada en el origen es $ [0,1] $.
· Su dominio es: $ D = ℝ $.
· Su codominio es: $ C = ℝ^{+} $.

Gráfico:

Función exponencial de base $ a > 1 $:

Características:
· Es una función decreciente.
· No tiene raíces: $ S = ∅ $
· Su ordenada en el origen es $ [0,1] $.
· Su dominio es: $ D = ℝ $.
· Su codominio es: $ C = ℝ^{+} $.

Gráfico:

Resolución de una ecuación exponencial:

· 1^er tipo: si son de igual base o se pueden llevar a igual base sin aplicar logaritmos:
$$ a^{p(x)} = a^{q(x)} ⇒ p(x) = q(x) $$
Se resuelve la ecuación a la que se ha llegado, su conjunto solución es el mismo del de la ecuación exponencial original.

· 2^do tipo: si son de distinta base y no se pueden llevar a la misma base sin aplicar logaritmos:
$$ a^{p(x)} = b^{q(x)} ⇒ [p(x)]·\ln(a) = [q(x)]·\ln(b) $$
Se aplican las distributivas necesarias (dependiendo de la función) y se lleva todo a un mismo miembro, luego, se ordenada en la variable y resuelve la ecuación, su conjunto solución es el mismo del de la ecuación exponencial original.

· 3^er tipo: si la ecuación exponencial es más compleja, entiéndase, que tiene más términos:
$$ p(x) + a^{q(x)} = 0 $$
Se aplica un cambio de variable conveniente.

· 4^to caso: si se trata de una suma de términos (progresión geométrica):
$$ a_{1} + a_{2} + a_{3} + ... + a^{x} = b $$
Se puede resolver fácilmente a través de la siguiente fórmula (deducida a partir de la de progresión geométrica):
$$ x = \log_{a} \left ( \frac {b·(a_{3}-a_{2})+a_{1}·a_{2}}{a_{3}} \right ) $$

· 5^to caso: si es sencilla, del tipo:
$$ a^{x} = b $$
Se aplica la definición de logaritmo:
$$ x = \log_{a} (b) $$

Página 1 de 1
1

Universo Científico

Admin

Admin

Admin

Admin