|
| Foro Departamento de Matemática Teóricos Función lineal o de primer grado |
| Función lineal o de primer grado |
|
11-04-2013, 7:36 PM
Post: #1
|
|||
|
|||
|
Función lineal o de primer grado:
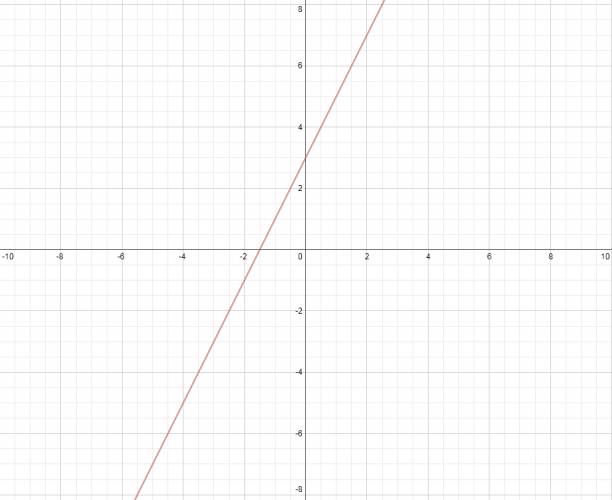
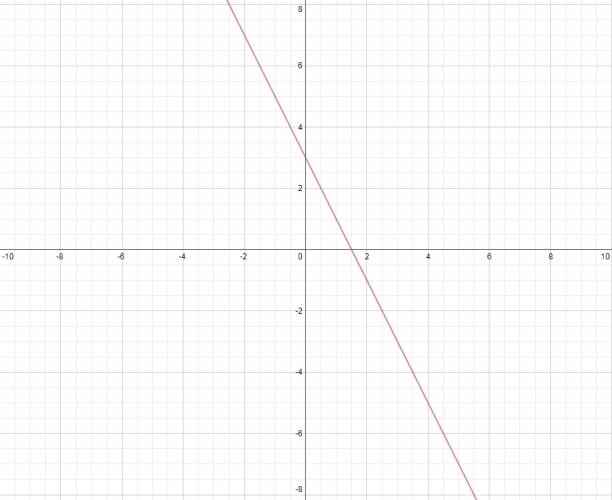
$$ f: ℝ → ℝ $$ Esto significa que le puedo dar cualquier valor real a la variable \( x \) y me devolverá otro valor real cualquiera. Es de la forma general: $$ f(x) = a·x + b $$ Con la condición de que \( a ≠ 0 \). · Raíz: Este tipo de funciones tienen una única raíz, que se calcula igualando el polinomio a 0. $$ a·x + b = 0 ⇒ x = - \frac {b}{a} $$ La raíz es el punto de corte de la función con el eje \( x \). · Ordenada en el origen: Es el punto de corte de la función con el eje \( y \). Se calcula como: \( f(0) = a·0 + b ⇒ f(0) = b \) La ordenada en el origen siempre es el término independiente (el que no tiene variable), en el caso de esta función, la ordenada en el origen siempre es el valor de \( b \). Quote Este tipo de funciones siempre tienen una recta como expresión gráfico en el plano. Inclinación: La inclinación de la recta está dada por el valor de \( a \) (el que multiplica a la variable). Diremos que \( a \) es la pendiente de la recta. El ángulo se puede calcular como: \( \tan (a) \). · Crecimiento: Una función polinómica de primer grado es creciente si la pendiente es positiva. $$ f(x) = 2·x + 3 $$ · Decrecimiento: Una función polinómica de primer grado es decreciente si la pendiente es negativa. $$ f(x) = -2·x + 3 $$ Una buena forma de graficar este tipo de funciones es conociendo la ordenada en el origen y la raíz, ya que su representación es una recta, y sólo existe una recta que pase por dos puntos (según Euclides). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
11-04-2013, 7:49 PM
Post: #2
|
|||
|
|||
|
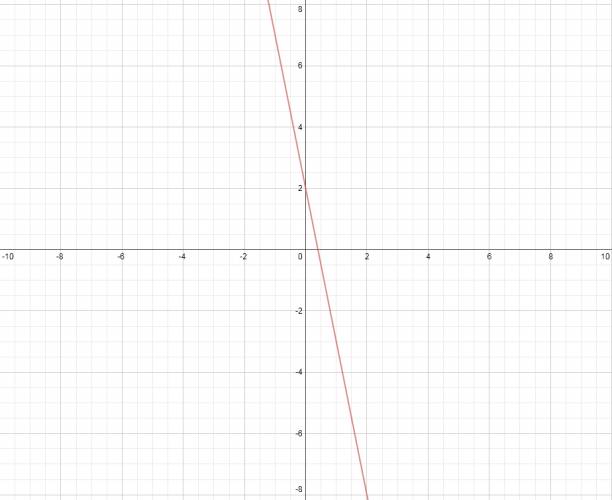
Ejemplo:
Sea la función: \( f(x) = -5·x +2 \) Sin ver el gráfico podemos afirmar que: · Tiene ordenada en el origen en 2. · Corta al eje \( x \) en \( \frac {2}{5} \). · Es decreciente. · El ángulo de inclinación es de \( -79º \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |