11-04-2013, 7:36 PM
Función lineal o de primer grado:
$$ f: ℝ → ℝ $$
Esto significa que le puedo dar cualquier valor real a la variable \( x \) y me devolverá otro valor real cualquiera.
Es de la forma general:
$$ f(x) = a·x + b $$
Con la condición de que \( a ≠ 0 \).
· Raíz:
Este tipo de funciones tienen una única raíz, que se calcula igualando el polinomio a 0.
$$ a·x + b = 0 ⇒ x = - \frac {b}{a} $$
La raíz es el punto de corte de la función con el eje \( x \).
· Ordenada en el origen:
Es el punto de corte de la función con el eje \( y \).
Se calcula como: \( f(0) = a·0 + b ⇒ f(0) = b \)
La ordenada en el origen siempre es el término independiente (el que no tiene variable), en el caso de esta función, la ordenada en el origen siempre es el valor de \( b \).
Inclinación:
La inclinación de la recta está dada por el valor de \( a \) (el que multiplica a la variable). Diremos que \( a \) es la pendiente de la recta.
El ángulo se puede calcular como: \( \tan (a) \).
· Crecimiento:
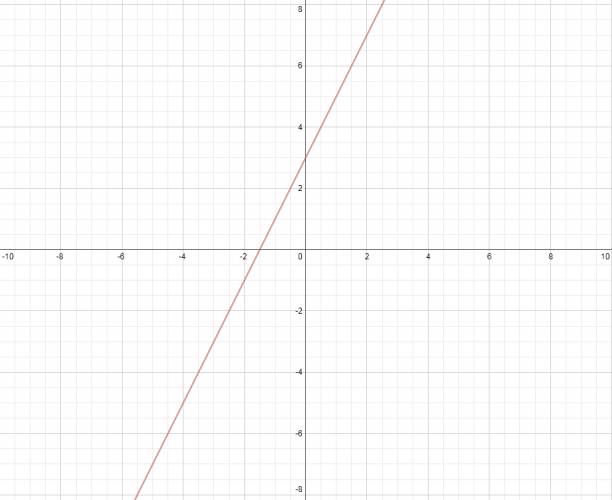
Una función polinómica de primer grado es creciente si la pendiente es positiva.
$$ f(x) = 2·x + 3 $$
· Decrecimiento:
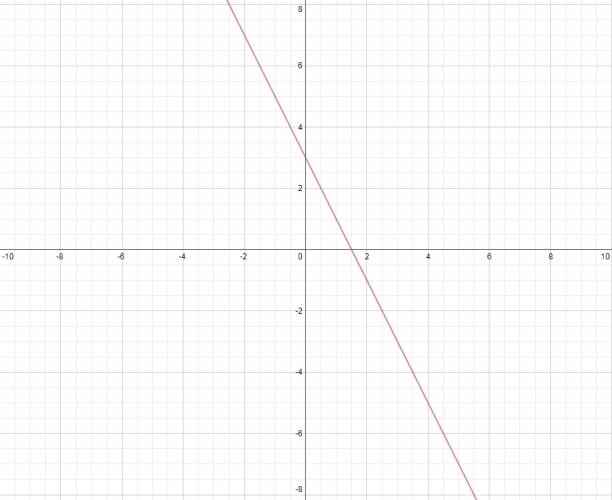
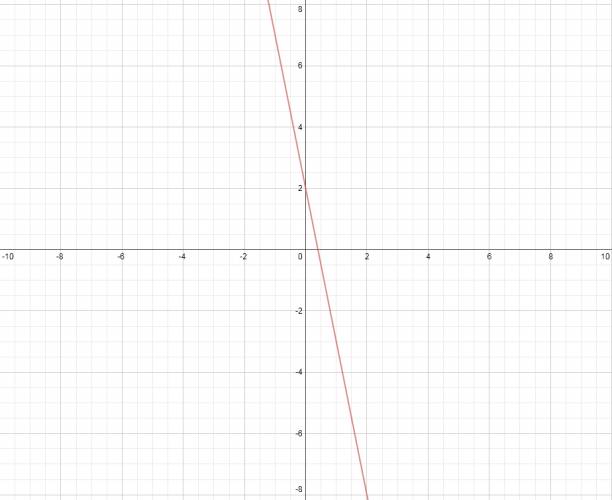
Una función polinómica de primer grado es decreciente si la pendiente es negativa.
$$ f(x) = -2·x + 3 $$
Una buena forma de graficar este tipo de funciones es conociendo la ordenada en el origen y la raíz, ya que su representación es una recta, y sólo existe una recta que pase por dos puntos (según Euclides).
$$ f: ℝ → ℝ $$
Esto significa que le puedo dar cualquier valor real a la variable \( x \) y me devolverá otro valor real cualquiera.
Es de la forma general:
$$ f(x) = a·x + b $$
Con la condición de que \( a ≠ 0 \).
· Raíz:
Este tipo de funciones tienen una única raíz, que se calcula igualando el polinomio a 0.
$$ a·x + b = 0 ⇒ x = - \frac {b}{a} $$
La raíz es el punto de corte de la función con el eje \( x \).
· Ordenada en el origen:
Es el punto de corte de la función con el eje \( y \).
Se calcula como: \( f(0) = a·0 + b ⇒ f(0) = b \)
La ordenada en el origen siempre es el término independiente (el que no tiene variable), en el caso de esta función, la ordenada en el origen siempre es el valor de \( b \).
Quote
Este tipo de funciones siempre tienen una recta como expresión gráfico en el plano.
Inclinación:
La inclinación de la recta está dada por el valor de \( a \) (el que multiplica a la variable). Diremos que \( a \) es la pendiente de la recta.
El ángulo se puede calcular como: \( \tan (a) \).
· Crecimiento:
Una función polinómica de primer grado es creciente si la pendiente es positiva.
$$ f(x) = 2·x + 3 $$
· Decrecimiento:
Una función polinómica de primer grado es decreciente si la pendiente es negativa.
$$ f(x) = -2·x + 3 $$
Una buena forma de graficar este tipo de funciones es conociendo la ordenada en el origen y la raíz, ya que su representación es una recta, y sólo existe una recta que pase por dos puntos (según Euclides).