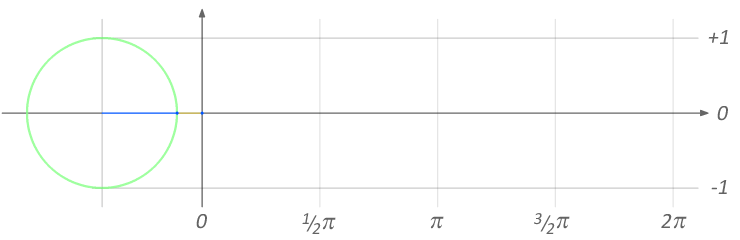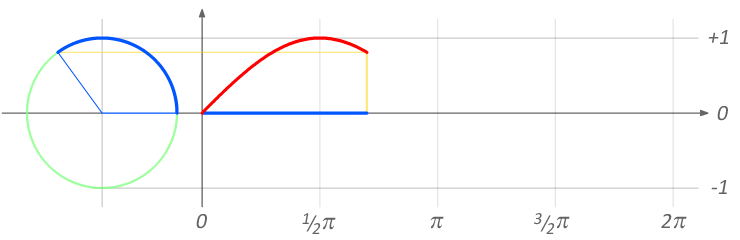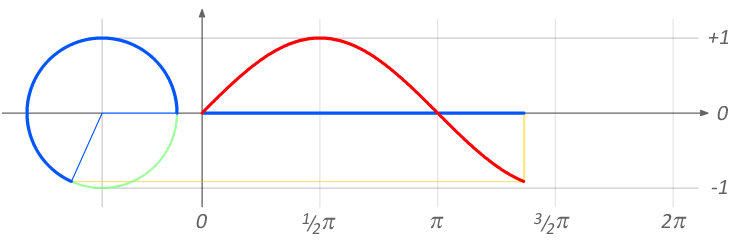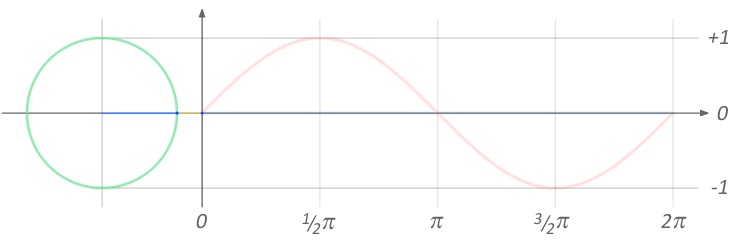|
   |
| Foro Departamento de Matemática Teóricos Funciones trigonométricas |
| Funciones trigonométricas |
|
19-03-2013, 9:50 PM
Post: #1
|
|||
|
|||
|
Las funciones trigonométricas, son las funciones de las identidades trigonométricas: seno, coseno, tangente, etc.
¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
  |
|
19-03-2013, 9:55 PM
Post: #2
|
|||
|
|||
|
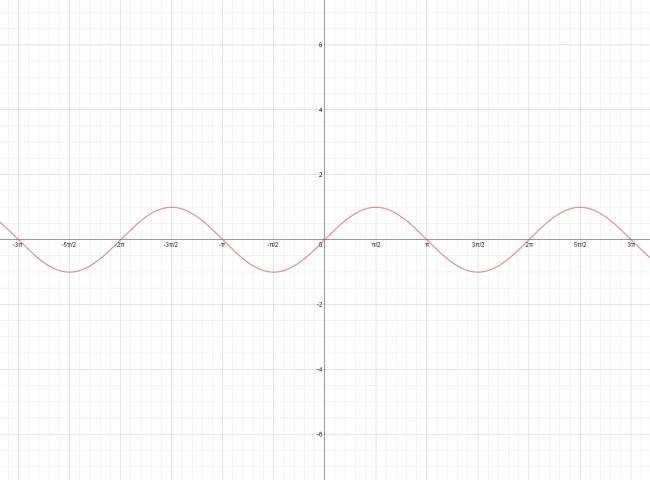
Función seno:
Características: · Función continua · Dominio: \( ℝ \) · Codominio: \( [-1; +1] \) · Periodo: \( 2·\pi \) Representación gráfica: $$ f(x) = \mbox{sen} x $$    ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
19-03-2013, 9:58 PM
Post: #3
|
|||
|
|||
|
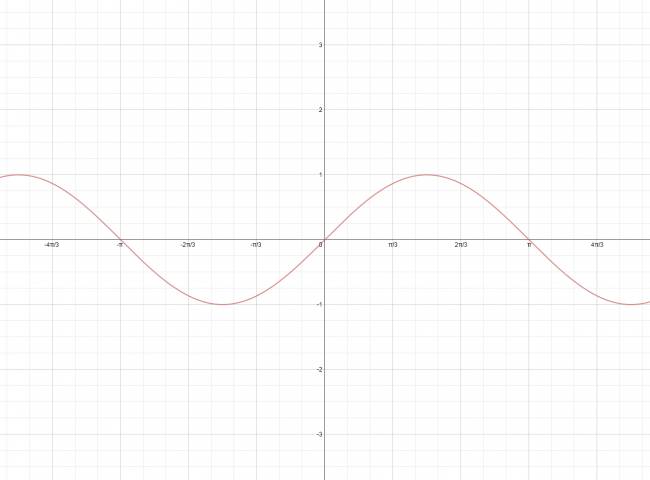
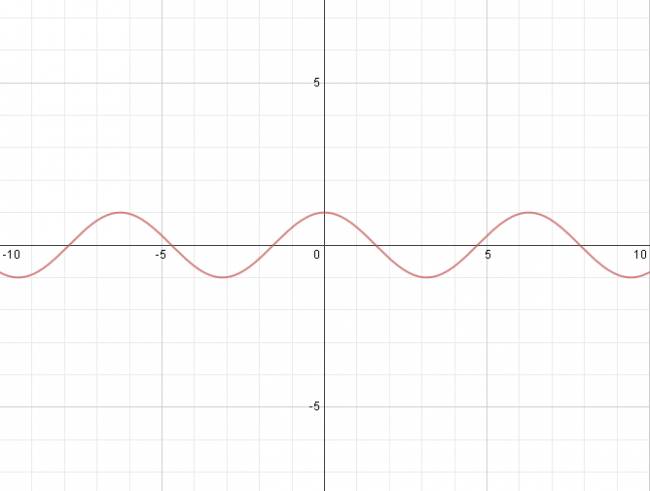
Función coseno:
Características: · Función continua · Dominio: \( ℝ \) · Codominio: \( [-1; +1] \) · Periodo: \( 2·\pi \) Representación gráfica: $$ f(x) = \mbox{cos} x $$  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
19-03-2013, 10:03 PM
Post: #4
|
|||
|
|||
|
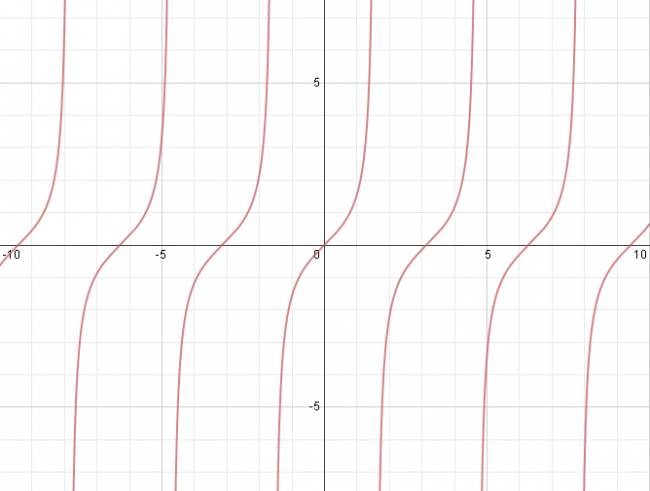
Función tangente:
Características: · Función no continua (presenta asíntotas verticales). · Dominio: \( ℝ - \left\{ (2·k + 1)·90, k∈ℤ \right\} \) · Codominio: \( ℝ \) Representación gráfica: $$ f(x) = \mbox{tan} x $$  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
28-03-2013, 12:09 PM
Post: #5
|
|||
|
|||
|
Función arcoseno:
Es la función inversa a la función seno. Características: · Función no continua. · Dominio: \( [-1, +1] \) · Codominio: \( [-\frac {\pi}{2}, +\frac {\pi}{2}] \) Representación gráfica: $$ f(x) = \mbox {sen}^{-1} x ∨ f(x) = \mbox {arcsen} x $$  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
28-03-2013, 12:14 PM
Post: #6
|
|||
|
|||
|
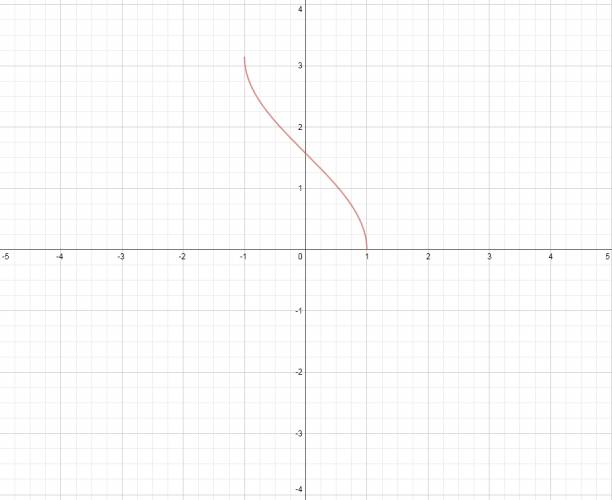
Función arcocoseno:
Es la función inversa a la función coseno. Características: · Función no continua. · Dominio: \( [-1, +1] \) · Codominio: \( [0, \pi] \) Representación gráfica: $$ f(x) = \mbox {cos}^{-1} x ∨ f(x) = \mbox {arccos} x $$  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
28-03-2013, 12:16 PM
Post: #7
|
|||
|
|||
|
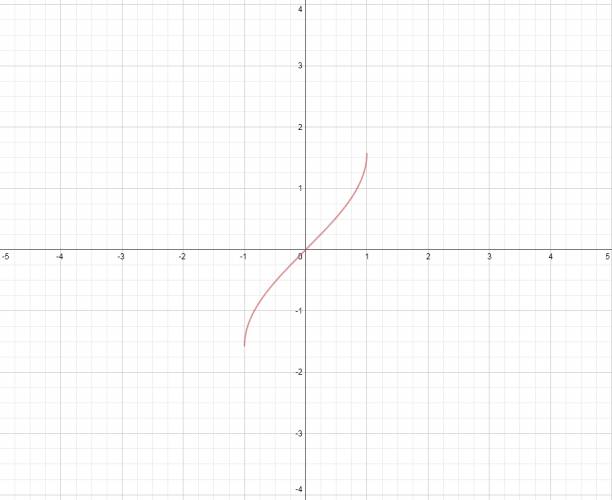
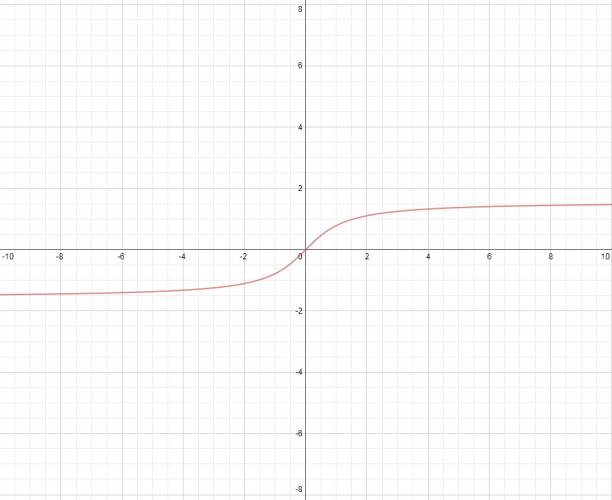
Función arcotangente:
Es la función inversa a la función tangente. Características: · Función continua. · Dominio: \( ℝ \) · Codominio: \( [-\frac {\pi}{2}, +\frac {\pi}{2}] \) Representación gráfica: $$ f(x) = \mbox {tan}^{-1} x ∨ f(x) = \mbox {arctan} x $$  Decimos que la función arcotangente tiene asíntotas horizontales \( y = ± \frac {\pi}{2} \), cuando los valores del dominio tienden a \( ± ∞ \), respectivamente. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |