|
   |
| Foro Departamento de Matemática Teóricos Vector |
| Vector |
|
27-02-2013, 11:08 PM
Post: #1
|
|||
|
|||
|
Un vector es un segmento de recta orientado que tiene dirección, punto de aplicación, sentido y módulo.
 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
  |
|
27-02-2013, 11:18 PM
Post: #2
|
|||
|
|||
|
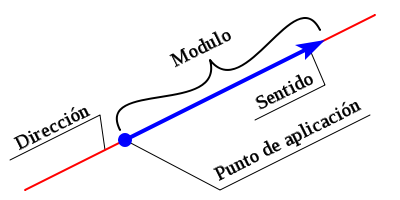
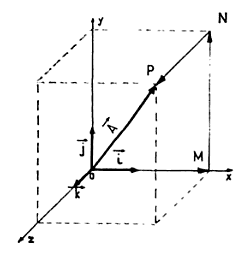
Vectores en el plano:
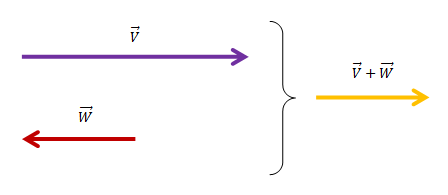
Vector en el plano denotado como \( ℝ^2 \). Vectores colineales: Son aquellos vectores que tienen la misma dirección. · Adición de vectores colineales: Se suman los módulos de los vectores que tienen el mismo sentido y se restan los módulos de los vectores que tienen sentido opuesto. Se conversa el sentido del vector o suma de vectores que tengan mayor módulo.  Vectores no-colineales: Son aquellos vectores que tienen diferente dirección. · Adición de vectores perpendiculares: Se puede aplicar el teorema de Pitágoras.  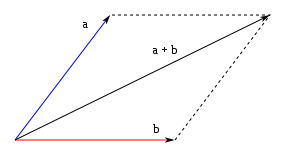Se puede considerar un cuadrado (sus dos diagonales son iguales) y para calcular cualquiera de las dos diagonales se puede utilizar el teorema de Pitágoras: $$ \vec {VW} = \vec V + \vec W = \sqrt {\vec V^2 + \vec W^2} $$ · Adición de vectores no-colineales y no-perpendiculares: · Método del paralelogramo:  El método analítico que se emplea para conocer el módulo del vector suma es una variante del teorema de coseno y para conocer el ángulo de inclinación se utiliza el teorema del seno. Variante del teorema de coseno: $$ \vec {ab} = \vec {a} + \vec {b} = \sqrt {a^2 + b^2 + 2·a·b· \cos \alpha} $$ Sea \( \alpha \) el ángulo de inclinación respecto a ambos. 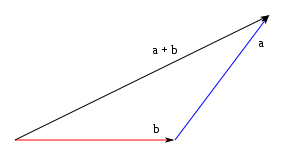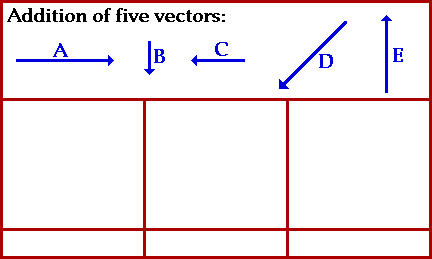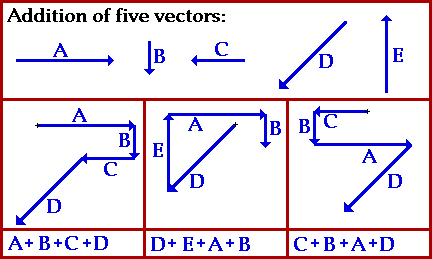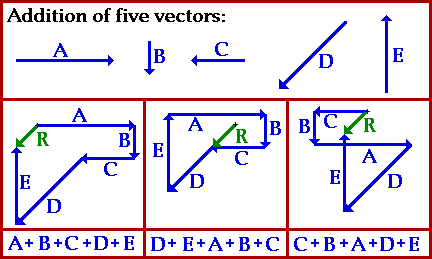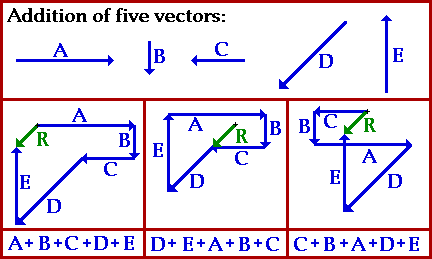· Método del triángulo:  Teorema de coseno: $$ \vec {ab} = \vec {a} + \vec {b} = \sqrt {a^2 + b^2 - 2·a·b· \cos \alpha} $$ Sea \( \alpha \) el ángulo de inclinación respecto a ambos. Toerema del seno: Lo puede ver en: http://ucientifico.ucoz.es/forum/15-69-1 En todos los casos, la adición de vectores es conmutativa.  · Principio de sustracción de vectores: Dos vectores se pueden restar, efectuando una suma, considerando al opuesto de uno de ellos: $$ \vec A - \vec B = \vec A + (- \vec B) $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
01-05-2013, 2:41 AM
Post: #3
|
|||
|
|||
|
Versores:
Se conocen como versores a los vectores de módulo igual a la unidad.  Los vectores unitarios reciben el nombre de \( i,j,k \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
01-05-2013, 8:05 PM
Post: #4
|
|||
|
|||
|
Vectores en el espacio:
Vector en el plano denotado como \( ℝ^3 \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |