|
| Foro Departamento de Matemática Teóricos Cotas, máximos y mínimos, extremos, supremo e ínfimo |
| Cotas, máximos y mínimos, extremos, supremo e ínfimo |
|
06-11-2012, 8:35 PM
Post: #1
|
|||
|
|||
|
Cota superior:
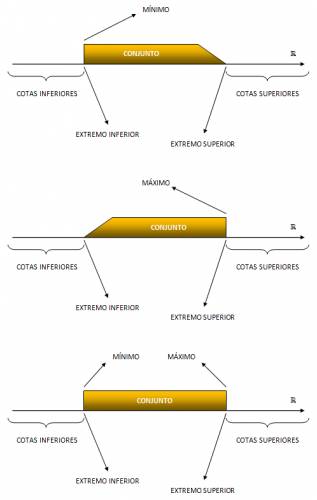
Definición: Dado un conjunto \( A \) de números reales, no vacío, diremos que \( k \) es cota superior del conjunto \( A \), si y sólo si, para todo \( x \) que pertenece a \( A \) se cumple que es menor o igual que \( k \). Con símbolos matemáticos: \( k \) es cota superior de \( A ⇔ ∃x, x∈A ∧ ∀x ⇒ x≤k \) Observaciones: · Si existe \( k \) en las condiciones anteriores, decimos que \( A \) está acotado superiormente. Cota inferior: Definición: Dado un conjunto \( A \) de números reales, no vacío, diremos que \( k \) es cota inferior del conjunto \( A \), si y sólo si, para todo \( x \) que pertenece a \( A \) se cumple que es mayor o igual que \( k \). Con símbolos matemáticos: \( k \) es cota inferior de \( A ⇔ ∃x, x∈A ∧ ∀x ⇒ x≥k \) Observaciones: · Si existe \( k \) en las condiciones anteriores, decimos que \( A \) está acotado inferiormente. · Si el conjunto \( A \) se encuentra acotado tanto superior como inferiormente, decimos que el conjunto \( A \) se encuentra acotado. Ejemplo: El conjunto de los números naturales \( (ℕ) \) está acotado inferiormente. Máximo: Definición: Dado un conjunto \( A \) de números reales, no vacío, diremos que \( M \) es máximo del conjunto \( A \), si y sólo si, \( M \) pertenece al conjunto \( A \) y es cota superior del mismo. Con símbolos matemáticos: $$ M = \mbox{máx} (A) ⇔ \begin{cases} M∈A \\ ∃x, x∈A ∧ ∀x ⇒ x≤M \end{cases} $$ Mínimo: Definición: Dado un conjunto \( A \) de números reales, no vacío, diremos que \( m \) es mínimo del conjunto \( A \), si y sólo si, \( m \) pertenece al conjunto \( A \) y es cota inferior del mismo. Con símbolos matemáticos: $$ m = \mbox{mín} (A) ⇔ \begin{cases} m∈A \\ ∃x, x∈A ∧ ∀x ⇒ x≥m \end{cases} $$ Extremo superior o supremo: Definición: Es la menor de las cotas superiores. También se le conoce como supremo. Extremo inferior o ínfimo: Definición: Es la mayor de las cotas inferiores. También se le conoce como ínfimo. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
23-03-2013, 1:25 AM
Post: #2
|
|||
|
|||
|
Cuando se trata de un intervalo:
Primer caso: \( (a,b) \) cota = x ≥ b cota = x ≤ a extr = b extr = a M = no tiene. m = no tiene. Segundo caso: \( (a,b] \) cota = x ≥ b cota = x ≤ a extr = b extr = a M = b m = no tiene. Tercer caso: \( [a,b) \) cota = x ≥ b cota = x ≤ a extr = b extr = a M = no tiene. m = a Cuarto caso: \( [a,b] \) cota = x ≥ b cota = x ≤ a extr = b extr = a M = b m = a Quinto caso: \( [a,+∞) \) cota = no tiene. cota = x ≤ a extr = no tiene. extr = a M = no tiene. m = a Sexto caso: \( (a,+∞) \) cota = no tiene. cota = x ≤ a extr = no tiene. extr = a M = no tiene. m = no tiene. Séptimo caso: \( (-∞,b] \) cota = x ≥ a cota = no tiene. extr = b extr = no tiene. M = b m = no tiene. Octavo caso: \( (-∞,b) \) cota = x ≥ a cota = no tiene. extr = b extr = no tiene. M = no tiene. m = no tiene. Noveno caso: \( (-∞,+∞) \) cota = no tiene. cota = no tiene. extr = no tiene. extr = no tiene. M = no tiene. m = no tiene. Quote Referencias: cota = cota superior cota = cota inferior extr = extremo superior o supremo extr = extremo inferior o ínfimo M = máximo m = mínimo · En todos los casos: \( x \) es un número real cualquiera que pertenece al intervalo estudiado. · En todos los casos: \( a \) y \( b \) son números reales cualesquiera. Observaciones: · Un intervalo no está acotado si es infinito en por lo menos uno de sus extremos de intervalo. · Si no tiene supremo no va a tener máximo. · Si no tiene ínfimo no va a tener mínimo. · No tiene supremo si es de la forma: [a,+∞) ó (a,+∞). · No tiene ínfimo si es de la forma: (-∞,a] ó (-∞,a). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
28-03-2013, 11:40 PM
Post: #3
|
|||
|
|||
|
Axioma de completitud o del extremo superior:
Enunciado: Todo conjunto de números reales, no vacío, acotado superiormente tiene supremo. Esta afirmación no se cumple en otros conjuntos como puede ser el caso de los números racionales. Veamos el siguiente ejemplo: $$ A = ℚ∩[-π,π] $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
02-04-2013, 1:36 PM
Post: #4
|
|||
|
|||
|
Conjunto de intervalo acotado:
¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |