06-11-2012, 8:35 PM
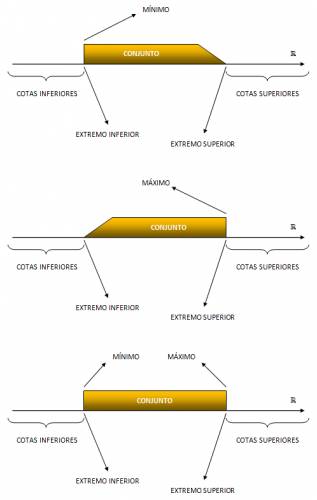
Cota superior:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( k \) es cota superior del conjunto \( A \), si y sólo si, para todo \( x \) que pertenece a \( A \) se cumple que es menor o igual que \( k \).
Con símbolos matemáticos:
Observaciones:
· Si existe \( k \) en las condiciones anteriores, decimos que \( A \) está acotado superiormente.
Cota inferior:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( k \) es cota inferior del conjunto \( A \), si y sólo si, para todo \( x \) que pertenece a \( A \) se cumple que es mayor o igual que \( k \).
Con símbolos matemáticos:
Observaciones:
· Si existe \( k \) en las condiciones anteriores, decimos que \( A \) está acotado inferiormente.
· Si el conjunto \( A \) se encuentra acotado tanto superior como inferiormente, decimos que el conjunto \( A \) se encuentra acotado.
Ejemplo:
El conjunto de los números naturales \( (ℕ) \) está acotado inferiormente.
Máximo:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( M \) es máximo del conjunto \( A \), si y sólo si, \( M \) pertenece al conjunto \( A \) y es cota superior del mismo.
Con símbolos matemáticos:
$$ M = \mbox{máx} (A) ⇔ \begin{cases} M∈A \\ ∃x, x∈A ∧ ∀x ⇒ x≤M \end{cases} $$
Mínimo:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( m \) es mínimo del conjunto \( A \), si y sólo si, \( m \) pertenece al conjunto \( A \) y es cota inferior del mismo.
Con símbolos matemáticos:
$$ m = \mbox{mín} (A) ⇔ \begin{cases} m∈A \\ ∃x, x∈A ∧ ∀x ⇒ x≥m \end{cases} $$
Extremo superior o supremo:
Definición:
Es la menor de las cotas superiores. También se le conoce como supremo.
Extremo inferior o ínfimo:
Definición:
Es la mayor de las cotas inferiores. También se le conoce como ínfimo.
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( k \) es cota superior del conjunto \( A \), si y sólo si, para todo \( x \) que pertenece a \( A \) se cumple que es menor o igual que \( k \).
Con símbolos matemáticos:
\( k \) es cota superior de \( A ⇔ ∃x, x∈A ∧ ∀x ⇒ x≤k \)
Observaciones:
· Si existe \( k \) en las condiciones anteriores, decimos que \( A \) está acotado superiormente.
Cota inferior:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( k \) es cota inferior del conjunto \( A \), si y sólo si, para todo \( x \) que pertenece a \( A \) se cumple que es mayor o igual que \( k \).
Con símbolos matemáticos:
\( k \) es cota inferior de \( A ⇔ ∃x, x∈A ∧ ∀x ⇒ x≥k \)
Observaciones:
· Si existe \( k \) en las condiciones anteriores, decimos que \( A \) está acotado inferiormente.
· Si el conjunto \( A \) se encuentra acotado tanto superior como inferiormente, decimos que el conjunto \( A \) se encuentra acotado.
Ejemplo:
El conjunto de los números naturales \( (ℕ) \) está acotado inferiormente.
Máximo:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( M \) es máximo del conjunto \( A \), si y sólo si, \( M \) pertenece al conjunto \( A \) y es cota superior del mismo.
Con símbolos matemáticos:
$$ M = \mbox{máx} (A) ⇔ \begin{cases} M∈A \\ ∃x, x∈A ∧ ∀x ⇒ x≤M \end{cases} $$
Mínimo:
Definición:
Dado un conjunto \( A \) de números reales, no vacío, diremos que \( m \) es mínimo del conjunto \( A \), si y sólo si, \( m \) pertenece al conjunto \( A \) y es cota inferior del mismo.
Con símbolos matemáticos:
$$ m = \mbox{mín} (A) ⇔ \begin{cases} m∈A \\ ∃x, x∈A ∧ ∀x ⇒ x≥m \end{cases} $$
Extremo superior o supremo:
Definición:
Es la menor de las cotas superiores. También se le conoce como supremo.
Extremo inferior o ínfimo:
Definición:
Es la mayor de las cotas inferiores. También se le conoce como ínfimo.