| Foro Departamento de Matemática Teóricos Funciones polinómicas |
| Funciones polinómicas |
|
26-02-2013, 6:01 PM
Post: #11
|
|||
|
|||
|
Raíces evidentes:
Primera raíz evidente: "Una función polinómica tiene raíz evidente \( x = 0 \), si y sólo si su término independiente es cero." Segunda raíz evidente: "Una función polinómica tiene raíz evidente \( x = 1 \), si y sólo si la suma de sus coeficientes es igual a cero." Tercera raíz evidente: "Una función polinómica tiene raíz evidente \( x = -1 \), si y sólo si la suma de sus coeficientes de los términos con exponente par de la variable, es igual a la suma de los coeficientes de los términso de exponente impar." ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-03-2013, 0:11 AM
Post: #12
|
|||
|
|||
|
Estudio del signo de una función polinómica:
1. Se hallan las raíces del polinomio. 2. Se ordenan de menor a mayor las raíces, siguiendo el siguiente esquema:  Los signos se ponen en el primer casillero de la derecha y se van alternando. Siendo: · \( \alpha \) = una de las raíces. · \( \beta \) = otra de las raíces. · \( sg(a) \) = signo del coeficiente principal (si es positivo o negativo). Recordar que: \( \alpha < \beta \) A modo de ejemplo: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
15-03-2013, 10:18 PM
Post: #13
|
|||
|
|||
|
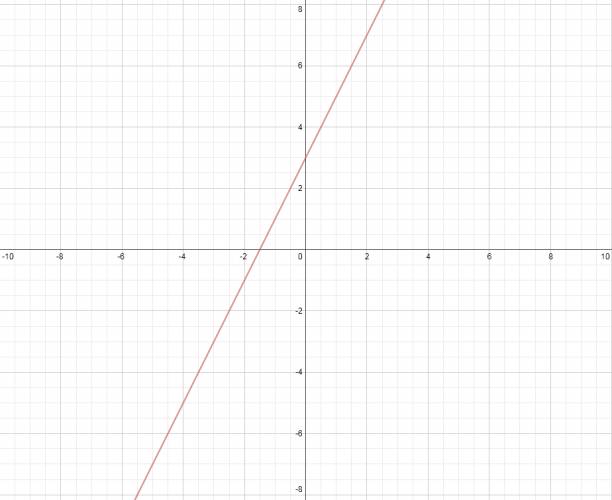
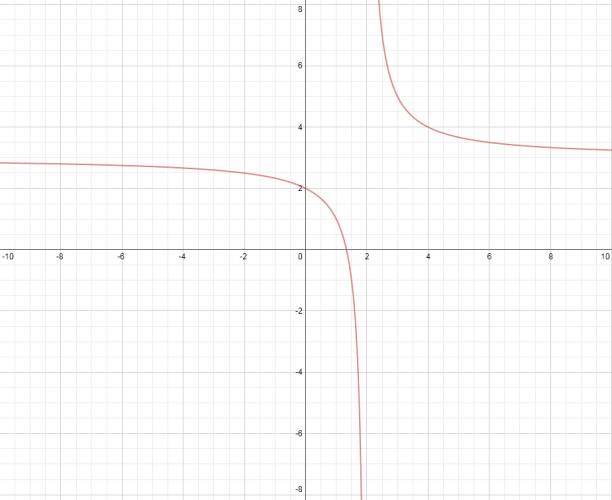
Dominio de una función:
El dominio de una función \( f(x) \) es el conjunto de todos los posibles valores por los que yo puedo reemplazar \( x \) por ese número. Seguramente más de uno no entendió nada, por eso vamos a poner ejemplos bien claros: · Función de primer grado: Veamos una función de primer grado: \( f(x) = 2·x + 3 \), ahora me pregunto, ¿puedo sustituir \( x \) por el número que yo quiera? La resputa es sí, ya que no hay nada que me lo impida, por esta razón decimos que en toda función lineal de primer grado de la forma\( f(x) = a·x + b \) el dominio es el conjunto de los números reales: \( D = ℝ \). · Función racional: Acá la cosa es un poco diferente, veamos por ejemplo la función racional: $$ f(x) = \frac {3·x - 4}{x - 2} $$ Y nos volvemos a hacer la pregunta de antes, ¿puedo sustituir \( x \) por el número que yo quiera? Y acá la respuesta es no. Recordemos que una fracción es una división y la parte de abajo de una fracción (denominador) nunca puede ser 0. Si yo resuelvo la ecuación del denominador: $$ x - 2 = 0 ⇒ x = 2 $$ Hallo el número real que hace que el denominador sea 0, en efecto: $$ f(2) = \frac {3·2 - 4}{2 - 2} = \frac {2}{0} $$ Y esto no puede ser, por lo que decimos que el dominio de la función es el conjunto de los números reales excepto ese número, expresado de una forma más formal sería: \( D = ℝ - \left\{ 2 \right\} \). Esto lo podemos ver de una forma gráfica: · Función de primer grado: Vemos que la recta es continua, no se corta nunca y a la vez sabemos que tiene una pendiente, o sea, está inclinada. A cada punto en horizontal le corresponde siempre uno en vertical y por esto es continua. · Función racional: Como vemos, la función no es continua, más precisamente no pasa por el punto de abscisa 2, vemos como que lo "evita". ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
15-03-2013, 10:48 PM
Post: #14
|
|||
|
|||
|
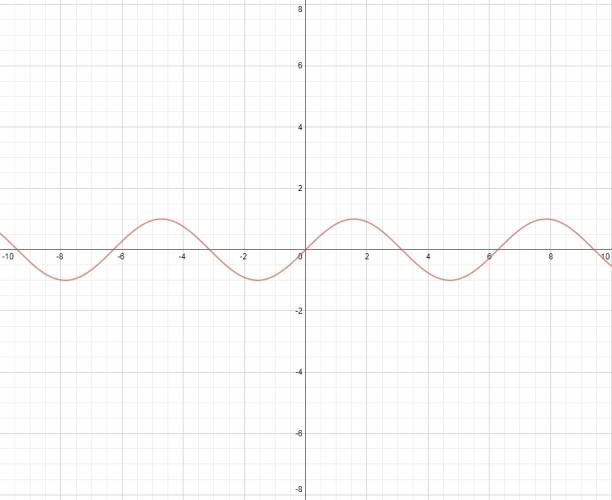
Codominio de una función:
El codominio de una función \( f(x) \) es el conjunto de todos los posibles valores por los que yo, una vez de haber sustituido por un valor de \( x \) tengo un valor de \( y \), más precisamente es el conjunto de todos los valores \( y \) (valores en vertical) que posee una función. Vamos a ejemplificar un poco para entender qué es esto. · Función de primer grado: Consideremos la función \( f(x) = 2·x + 3 \), siempre que yo sustituyo \( x \) por un número cualquiera tenemos un número que resulta de hacer la cuenta, la pregunta es: ¿existe algún valor que no resulte de hacer esa cuenta cuando yo sustituyo \( x \) por cualquier número? La respuesta en no, y esto se debe a que las funciones de la forma \( f(x) = a·x + b \) tiene codominio real: \( C = ℝ \). · Función seno: Acá es cuando la cosa cambia. Consideremos la función: \( f(x) = sen (x) \). Cuando yo sustituyo \( x \) por un valor que yo quiera, ¿qué valores resultan como resultado? Y bueno, la respuesta no es el conjunto de los número reales, es mucho más limitado, si probamos con la calculadora científica los valores que queramos de \( x \) veremos que los resultados no son menores que -1 ni mayores que +1, sino que está limitado entre estos valores (incluidos estos). Diremos que el codominio de esta función es: \( C = [-1; +1] \). Acá grafico la función seno para que se vea de qué hablo: Como vemos, la gráfica nunca tiene una altura superior a +1 ni inferior a -1. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
18-03-2013, 4:22 AM
Post: #15
|
|||
|
|||
|
Distintos tipos de funciones algebraicas:
· Función constante: es aquella función que es un número real (no interviene ninguna variable), es paralela al eje \( x \) y es siempre horizontal. Forma general: \( f(x) = k, k∈ℝ \). Ejemplo: \( f(x) = 3 \) · Función exponencial: es aquella función de base fija y exponente variable. Forma general: \( f(x) = a^{x}, a∈ℝ^{*} \). · Función logarítmica: es de la forma \( \log_{a} x, a>0, a≠1 \). · Función racional: es una función en la que la incógnita está en el denominador de una fracción. No es una función continua. Generalmente su forma es: \( f(x) = \frac {a·x + b}{c·x + d}, a·d≠b·c \). · Función radical: son aquellas funciones en donde la variable está bajo el signo de radical. Ejemplo: \( f(x) = \sqrt {x+1} \). · Función trigonométrica: son aquellas funciones en que las identidades trigonométricas (seno, coseno, tangente, etc) están aplicadas a una variable. Ejemplo: \( f(x) = \cos x \). · Función de valor absoluto (o de módulo): son aquellas funciones donde se aplica el valor absoluto a la variable. Ejemplo: \( f(x) = |x+2| \). · Función a trozos: son funciones compuestas por dos o más funciones pero que se grafican en determinados lugares (bajo condicionales). Ejemplo: $$ f(x) = \begin{cases} -2·x \mbox{ si } x≤0 \\ -x^2 + 4·x \mbox{ si } x>0 \end{cases} $$ · Función lineal o de primer grado: es una función de la forma \( f(x) = a·x + b, a≠0, (a,b)∈ℝ \). Su función es una recta que no es paralela a ninguna de los ejes, sino que tiene un inclinación (pendiente). · Función cuadrática o de segundo grado: es una función de la forma \( f(x) = a·x^2 + b·x + c, a≠0, (a,b,c)∈ℝ \). Su función es una parábola. · Función cúbica o de tercer grado: es una función de la forma \( f(x) = a·x^3 + b·x^2 + c·x + d, a≠0, (a,b,c,d)∈ℝ \). No tiene una forma única de representación. · Función de cuarto grado: es una función de la forma \( f(x) = a·x^4 + b·x^3 + c·x^2 + d·x + e, a≠0, (a,b,c,d,e)∈ℝ \). No tiene una forma única de representación. · Función polinómica general: \( f(x) = a_{0}·x^{n} + a_{1}·x^{n-1} + ... + a_{n-1}·x + a_{n}, a_{0}≠0, a∈ℝ \) ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |