|
| Foro Departamento de Física Problemas resueltos Problema de encuentro en MRU (separación) |
| Problema de encuentro en MRU (separación) |
|
19-04-2013, 11:23 PM
Post: #1
|
|||
|
|||
|
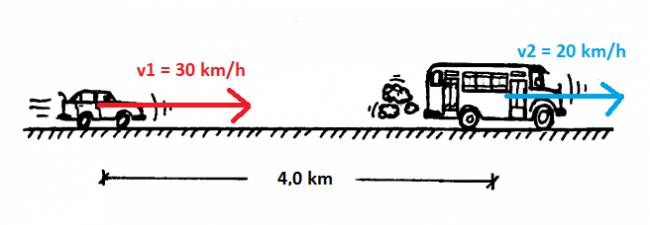
dos ciclistas se mueven en el mismo sentido por una carretera uno lo hace con una velocidad constante de 20 k/h y otro q procura alcanzarlo lo hace con una velocidad de 30k/h
¿cuanto tiempo trancurre antes de q se encuentren si inicialmente su separacion es de 4 kilometros? |
|||
|
19-04-2013, 11:41 PM
Post: #2
|
|||
|
|||
|
Es un problema de encuentro de MRU (velocidad constante en ambos casos). Hay que tener presente que la condición de encuentro es que se encuentren en un mismo lugar al mismo tiempo. Condición de encuentro: $$ x_{f1} = x_{f2} $$ $$ t_{f1} = t_{f2} $$ Vamos a calcular el momento de encuentro de ambos móviles, para esto vamos a utilizar la única fórmula de este movimiento y la vamos a despejar. Móvil 1: $$ v_{x1} = \frac {\Delta x}{\Delta t} ⇒ \Delta x = v_{x1}·\Delta t ⇒ x_{f} - x_{i} = v_{x1}·(t_{f} - t_{i}) ⇒ x_{f} = v_{x1}·t_{f} $$ Aclaraciones: · Como ambos móviles parten al mismo tiempo, puedo afirmar que \( t_{i} = 0,0 s \). · El primer móvil parte desde el origen: \( x_{i} = 0,0 km \). Reemplazando los datos, resulta en: $$ x_{f} = 30 \frac {km}{h}·t_{f} $$ Móvil 2: $$ v_{x1} = \frac {\Delta x}{\Delta t} ⇒ \Delta x = v_{x1}·\Delta t ⇒ x_{f} - x_{i} = v_{x1}·(t_{f} - t_{i}) ⇒ x_{f} - x_{i} = v_{x1}·t_{f} $$ Aclaraciones: · Como ambos móviles parten al mismo tiempo, puedo afirmar que \( t_{i} = 0,0 s \). $$ x_{f} - x_{i} = v_{x1}·t_{f} ⇒ x_{f} - 4,0 km = 20 \frac {km}{h}·t_{f} ⇒ x_{f} = 20 \frac {km}{h}·t_{f} + 4,0 km $$ Ahora, vamos a igualar la ecuaciones: $$ 30 \frac {km}{h}·t_{f} = 20 \frac {km}{h}·t_{f} + 4,0 km ⇒ 30 \frac {km}{h}·t_{f} - 20 \frac {km}{h}·t_{f} = 4,0 km ⇒ 10 \frac {km}{h}·t_{f} = 4,0 km ⇒ t_{f} = \frac {4,0 km}{10 \frac {km}{h}} ⇒ t_{f} = 0,4 h $$ Para hallar el lugar de encuentro, tenemos que reemplazar el tiempo en cualquiera de las dos ecuaciones de los móviles, no importa en cuál, ya que ambas nos darán lo mismo. Yo voy a reemplazar en la del móvil 1: $$ x_{f} = 30 \frac {km}{h}·t_{f} ⇒ x_{f} = 30 \frac {km}{h}·0,4 h ⇒ x_{f} = 12 km $$ Quote Respuesta expresada en unidades del SI (Sistema Internacional de Unidades): Ambos móviles se encontrarán a los \( 1,2·10^{4} m \) del origen, y a los \( 1,4·10^{3} s \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |