| Foro Problemas resueltos Problema de encuentro en MRU (separación) |
| Problema de encuentro en MRU (separación) |
19-04-2013, 11:23 PM
|
19-04-2013, 11:41 PM
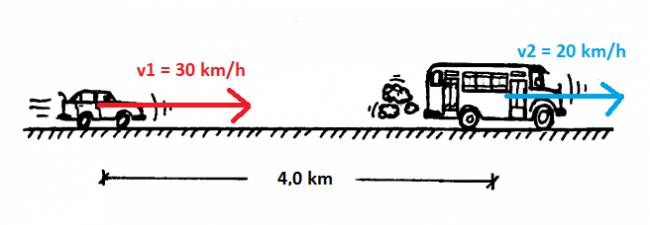
 Es un problema de encuentro de MRU (velocidad constante en ambos casos). Hay que tener presente que la condición de encuentro es que se encuentren en un mismo lugar al mismo tiempo. Condición de encuentro: $$ x_{f1} = x_{f2} $$ $$ t_{f1} = t_{f2} $$ Vamos a calcular el momento de encuentro de ambos móviles, para esto vamos a utilizar la única fórmula de este movimiento y la vamos a despejar. Móvil 1: $$ v_{x1} = \frac {\Delta x}{\Delta t} ⇒ \Delta x = v_{x1}·\Delta t ⇒ x_{f} - x_{i} = v_{x1}·(t_{f} - t_{i}) ⇒ x_{f} = v_{x1}·t_{f} $$ Aclaraciones: · Como ambos móviles parten al mismo tiempo, puedo afirmar que \( t_{i} = 0,0 s \). · El primer móvil parte desde el origen: \( x_{i} = 0,0 km \). Reemplazando los datos, resulta en: $$ x_{f} = 30 \frac {km}{h}·t_{f} $$ Móvil 2: $$ v_{x1} = \frac {\Delta x}{\Delta t} ⇒ \Delta x = v_{x1}·\Delta t ⇒ x_{f} - x_{i} = v_{x1}·(t_{f} - t_{i}) ⇒ x_{f} - x_{i} = v_{x1}·t_{f} $$ Aclaraciones: · Como ambos móviles parten al mismo tiempo, puedo afirmar que \( t_{i} = 0,0 s \). $$ x_{f} - x_{i} = v_{x1}·t_{f} ⇒ x_{f} - 4,0 km = 20 \frac {km}{h}·t_{f} ⇒ x_{f} = 20 \frac {km}{h}·t_{f} + 4,0 km $$ Ahora, vamos a igualar la ecuaciones: $$ 30 \frac {km}{h}·t_{f} = 20 \frac {km}{h}·t_{f} + 4,0 km ⇒ 30 \frac {km}{h}·t_{f} - 20 \frac {km}{h}·t_{f} = 4,0 km ⇒ 10 \frac {km}{h}·t_{f} = 4,0 km ⇒ t_{f} = \frac {4,0 km}{10 \frac {km}{h}} ⇒ t_{f} = 0,4 h $$ Para hallar el lugar de encuentro, tenemos que reemplazar el tiempo en cualquiera de las dos ecuaciones de los móviles, no importa en cuál, ya que ambas nos darán lo mismo. Yo voy a reemplazar en la del móvil 1: $$ x_{f} = 30 \frac {km}{h}·t_{f} ⇒ x_{f} = 30 \frac {km}{h}·0,4 h ⇒ x_{f} = 12 km $$ Quote Respuesta expresada en unidades del SI (Sistema Internacional de Unidades): Ambos móviles se encontrarán a los \( 1,2·10^{4} m \) del origen, y a los \( 1,4·10^{3} s \). |
Lo sentimos, pero sólo los usuarios registrados pueden tener acceso a este contenido. Si aún no eres usuario, puedes registrarte haciendo click aquí, y si ya lo eres, simplemente debes loguearte.