|
| Foro Departamento de Matemática Problemas resueltos Problema de complejos, módulo, hallar región del plano, cfa |
| Problema de complejos, módulo, hallar región del plano, cfa |
|
12-07-2013, 4:34 PM
Post: #1
|
|||
|
|||
|
Hallar el conjunto de los números \( z \) del plano complejo que satisfacen que \( | z + i + 1 | = 2 \).
|
|||
|
12-07-2013, 4:41 PM
Post: #2
|
|||
|
|||
|
Primero que nada: sabemos que \( z \) representa un complejo cualquiera, y como vemos, estamos trabajando de forma puramente algebraica, por lo que nos corresponderá usar la notación binómica. Entonces afirmo lo siguiente:
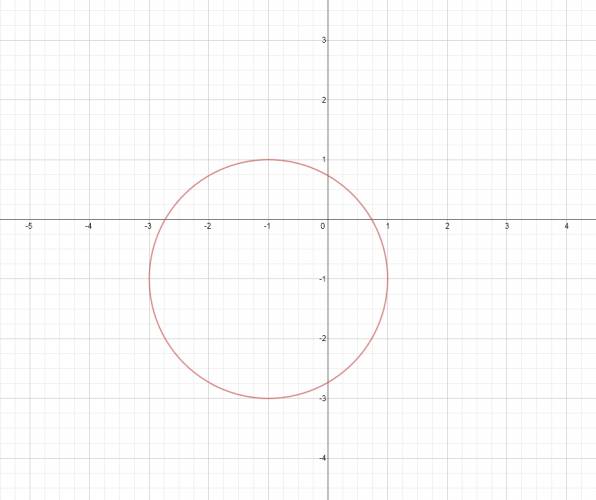
$$ z = a + b·i $$ Reemplazo en la ecuación: $$ | a + b·i + i + 1 | = 2 $$ Asocio términos a mi conveniencia: reales por un lado, imaginarios por el otro. $$ | (a + 1) + (b+1)·i | = 2 $$ Recordemos que el módulo de un complejo se puede calcular de la forma: $$ | z | = \sqrt {x^2 + y^2} $$ Aplico el anterior razonamiento a la ecuación: $$ \sqrt {(x+1)^2 + (y+1)^2} = 2 $$ Elevo ambos miembros al cuadrado para sacarme el radical: $$ (x+1)^2 + (y+1)^2 = 4 $$ Hago potencia, distributiva, todo lo que me convenga y lo dejo todo de un solo lado: $$ x^2 + y^2 + 2·x + 2·y - 2 = 0 $$ La anterior ecuación corresponde a una cfa de centro \( C(-1, -1) \) y radio \( r=2 \). Ahora la grafico: Recordemos que los valores de \( x \) son los valores reales, mientras que los valores de \( y \) son los valores imaginarios. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |