|
| Foro Departamento de Matemática Problemas resueltos Problemas de programación lineal (II) |
| Problemas de programación lineal (II) |
|
24-04-2013, 11:09 PM
Post: #1
|
|||
|
|||
|
24-04-2013, 11:21 PM
Post: #2
|
|||
|
|||
|
Primer problema:
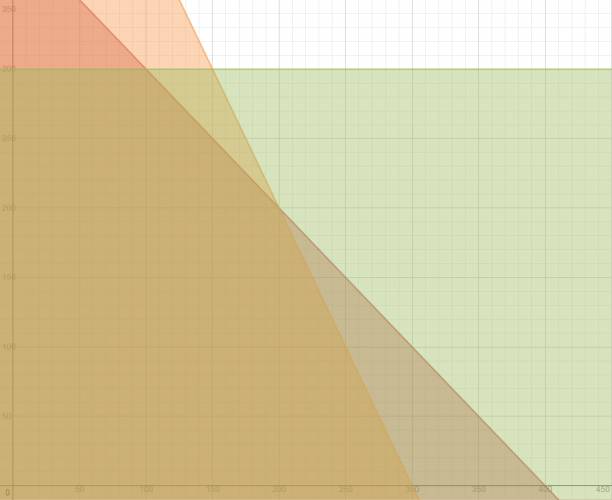
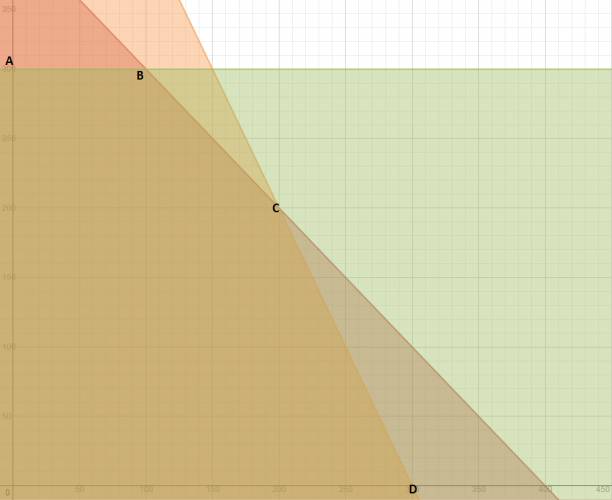
Hay que sacar los datos del problema, lo que a mí me gusta hacer es un cuadrito de doble entrada con los datos: 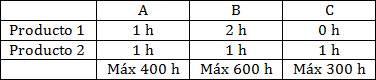 Voy a llamar: \( x \): producto 1 \( y \): producto 2 Y la función objetivo la saco del problema: $$ F(x,y) = 50·x + 80·y $$ Sacamos las restricciones del cuadro que puse más arriba, una de cada columna: Columna A: $$ x + y ≤ 400 $$ Columna B: $$ 2·x + y ≤ 600 $$ Columna C: $$ y ≤ 300 $$ Las graficamos: Ahora vamos a localizar los vértices, el origen no me importa porque ya sé que va a dar 0. $$ A (0,300) → F(0,300) = 24.000$$ $$ B (100,300) → F(100,300) = 29.000 $$ $$ C (200,200) → F(200,200) = 26.000 $$ $$ D (300,0) → F(300,0) = 15.000 $$ Como me pidieron maximizar, sé que es el B. $$ \frac {29.000}{100} = $290 $$ Lo más conveniente es producir 100 del producto 1 y 300 del 2. |
|||
|
24-04-2013, 11:44 PM
Post: #3
|
|||
|
|||
|
Segundo problema:
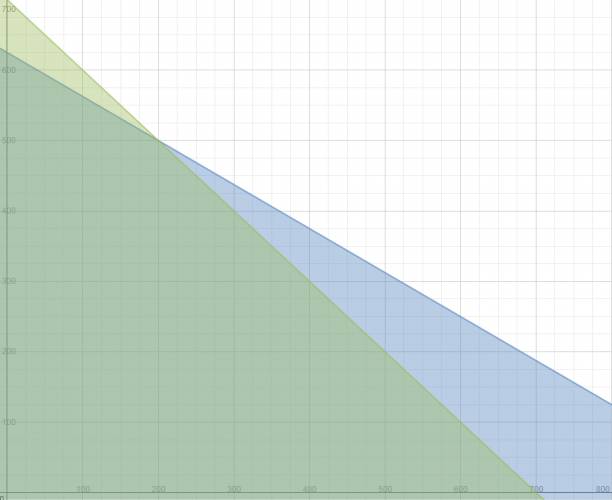
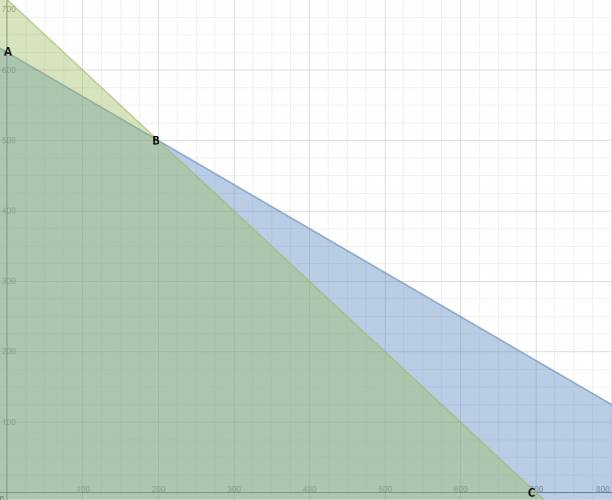
Este problema marea más que el otro, por lo que hay que abrir bien los ojos. Hay dos funciones objetivo: $$ F_{1} (x,y) = 5·x + 8·y $$ $$ F_{2} (x,y) = 13·x + 18·y $$ Siendo: \( x \): las naranjas del tipo A. \( y \): las naranjas del tipo B. Ahora vamos a sacar las restricciones del problema: $$ 5·x + 8·y ≤ 5.000 $$ $$ x + y ≤ 700 $$ Y lo vamos a graficar: Vamos a identificar los vértices del polígono. Calculamos con la segunda función objetivo: $$ A(0,625) → F(0,625) = 11.250 $$ $$ B(200,500) → F(200,500) = 11.600 $$ $$ C(700,0) → F(700,0) = 9.100 $$ Como me piden maximización, la respuesta es el vértice B. Cita Respuesta: Lo más conveniente es comprar 200 kg de las naranjas del tipo A, y 500 kg de las naranjas del tipo B. Ahora me piden cuánto va a ser el beneficio, el beneficio es lo que gana la persona, descontando la inversión que hizo. Calculamos el vértice B con la primer función objetivo: $$ B(200,500) → F(200,500) = 5.000 $$ La diferencia de esto es: $ 6.600, lo cual es la respuesta, lo que ganará. |
|||
|
25-04-2013, 0:04 AM
Post: #4
|
|||
|
|||
|
Tercer problema:
Cuadro de datos:  Variables: \( x \): crudo ligero \( y \): crudo pesado Restricciones: $$ 0,3·x + 0,3·y ≥ 900.000 $$ $$ 0,2·x + 0,4·y ≥ 800.000 $$ $$ 0,3·x + 0,2·y ≥ 500.000 $$ Graficamos: Identificamos los vértices: $$ A(0,3.000.000) → F(0,3.000.000) = 90 millones $$ $$ C(4.000.000,0) → F(4.000.000,0) = 140 millones $$ $$ B(2.000.000,1.000.000) → F(2.000.000,1.000.000) = 100 millones $$ Como me piden minimizar (menor costo), la respuesta es el vértice A. Cita Respuesta: Debe comprar 3 millones de barriles de crudo pesado y ninguno del ligero. Obtiene de esa manera un costo mínimo de 90 millones de dólares. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |