|
| Foro Departamento de Matemática Problemas resueltos Problema de función a trozos |
| Problema de función a trozos |
|
17-03-2013, 2:27 AM
Post: #1
|
|||
|
|||
|
1. Representar gráficamente:
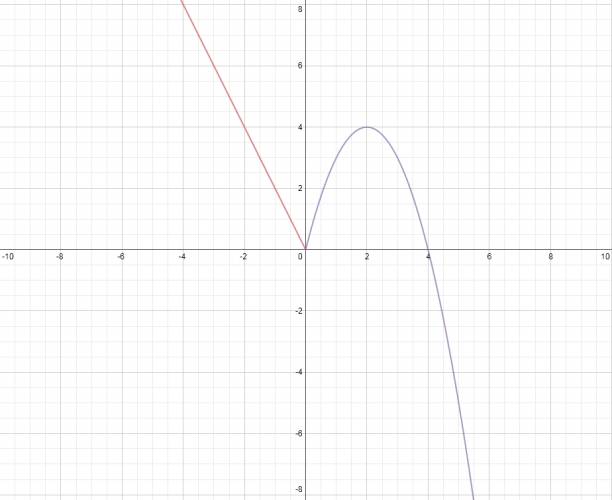
$$ f:f(x) = \begin{cases} -2·x \mbox{ si } x≤0 \\ -x^2 + 4·x \mbox{ si } x>0 \end{cases} $$ 2. Discutir según \( k∈ℝ \), el número de raíces de la ecuación \( f(x) = k \). 3. Representar gráficamente, en el mismo sistema de ejes que \( f \), la función \( t:t(x) = x^2 + 2·x - 24 \) y deducir signo \( (f(x) - t(x)) \). |
|||
|
18-03-2013, 2:25 AM
Post: #2
|
|||
|
|||
|
La graficamos:
¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
18-03-2013, 2:32 AM
Post: #3
|
|||
|
|||
|
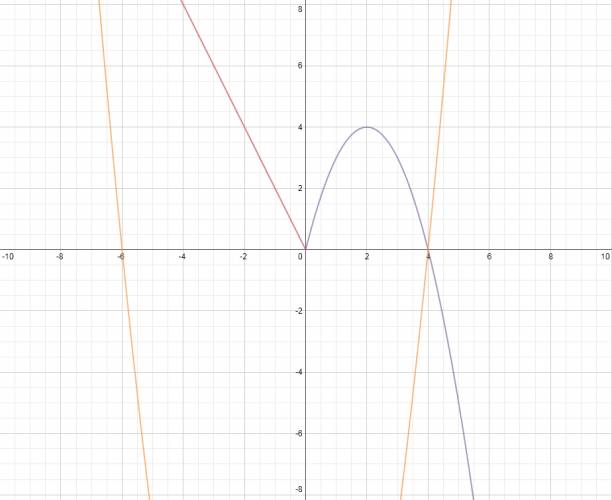
Quote (marcos364) 2. Discutir según k∈R. Cuando en matemática se me pide discutir lo que se quiere decir es que busque todos los casos posibles de una proposición y que vea si se cumple o no. Como lo dice la letra \( k \) es un número real, lo que tengo que hacer es una función de ese número, o sea, \( f(k) \). La función de un número real cualquiera es una función constate, esto significa que es una recta horizontal paralela al eje \( x \). Entonces, se me pide ver cuántas intersecciones (raíces) habría de la recta con la función \( f(x) \), o sea, cuántas veces se cortarían estas rectas. Quote Si \( k < 0 \) habrá una única raíz. Si \( k = 0 \) habrán dos raíces. Si \( k < k ≤ 4 \) habrán tres raíces. Si \( k > 4 \) habrá una única raíz. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
18-03-2013, 2:41 AM
Post: #4
|
|||
|
|||
|
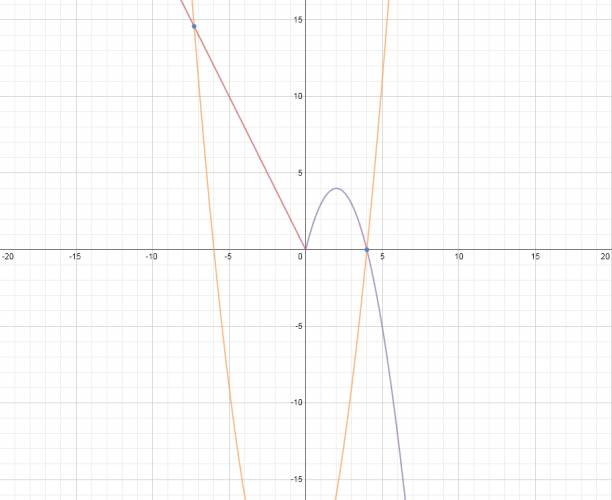
Quote (marcos364) 3. Representar gráficamente, en el mismo sistema de ejes que f, la función t:t(x)=x2+2⋅x−24 y deducir signo (f(x)−t(x)) Para deducir el signo, ante todo, tenemos que saber el punto en que se cortan ambas funciones. ¿Cómo hacemos esto? No es mucho misterio, tan solo tenemos que igualar las dos funciones que forman a \( f(x) \) a la función \( t(x) \). $$ x^2 + 2·x - 24 = -2·x ∧ x^2 + 2·x - 24 = -x^2 + 4·x $$ Resultando por un lado: $$ x^2 + 2·x - 24 = -2·x ⇒ x^2 + 4·x - 24 = 0 $$ Resolviendo por Bháskara llegamos a: $$ S = \left\{ -2-2· \sqrt {7}; -2+2· \sqrt {7} \right\} $$ Pero como la función lineal era sólo para los números negativos y el cero, debemos descartar la solución positiva. Resultando: $$ S = \left\{ -2-2· \sqrt {7}\right\} $$ Y por otro lado: $$ x^2 + 2·x - 24 = -x^2 + 4·x ⇒ 2·x^2 - 2·x -24 = 0 $$ Resolviendo por Bháskara llegamos a: $$ S = \left\{ -3; 4 \right\} $$ Pero como la función cuadrática era sólo para los números positivos debemos descartar la solución negativa. Resultando: $$ S = \left\{ 4 \right\} $$ En efecto, las grafico para verificar que sí son las raíces: Ahora que tenemos las raíces vamos a hacer el estudio del signo: ponemos las raíces de menor a mayor y pensamos. Luego del punto \( x = 4 \), ¿cómo es el signo de la la función resultante? Pues, ¡es negativo! Por esta razón comenzamos desde la izquierda y ponemos negativo y vamos alternando entre negativo y positivo, cada vez que pasa por una raíz cambia su signo. ¿Cómo sé que es negativo el signo después de dicho punto? Pues veamos, el término principal de la función \( f(x) \) es en todo momento negativo, mientras que el de la función \( t(x) \) es positivo, cuando restamos vamos a tener que \( -x^2 - (x^2) = - 2·x^2 \), pasaría también en el caso de la función lineal, más allá de que mi ejemplo haya sido de la función cuadrática. Quote Llegamos a que:  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |