Quote (marcos364)
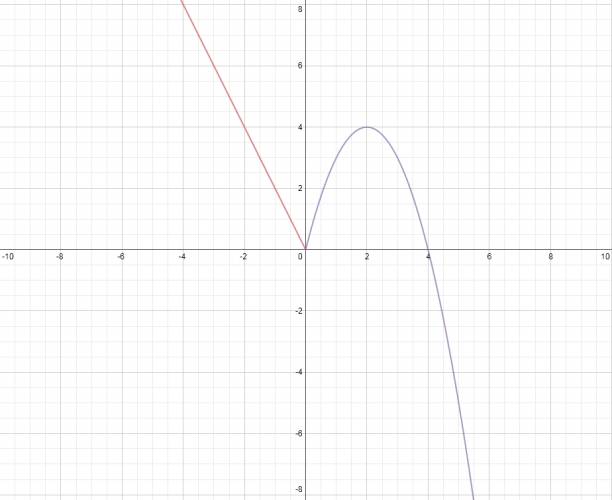
3. Representar gráficamente, en el mismo sistema de ejes que f, la función t:t(x)=x2+2⋅x−24 y deducir signo (f(x)−t(x))
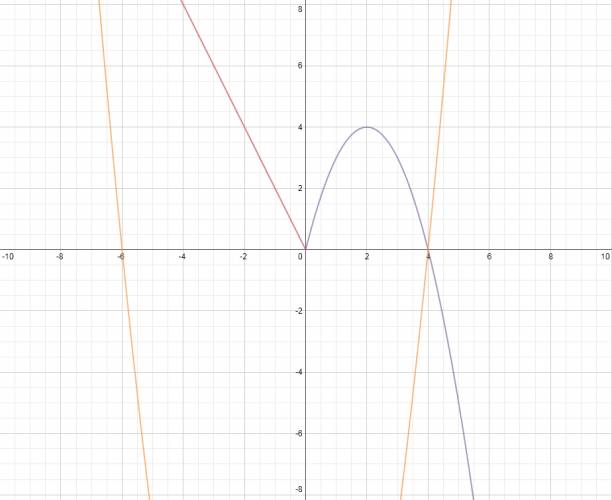
Para deducir el signo, ante todo, tenemos que saber el punto en que se cortan ambas funciones.
¿Cómo hacemos esto? No es mucho misterio, tan solo tenemos que igualar las dos funciones que forman a \( f(x) \) a la función \( t(x) \).
$$ x^2 + 2·x - 24 = -2·x ∧ x^2 + 2·x - 24 = -x^2 + 4·x $$
Resultando por un lado:
$$ x^2 + 2·x - 24 = -2·x ⇒ x^2 + 4·x - 24 = 0 $$
Resolviendo por Bháskara llegamos a:
$$ S = \left\{ -2-2· \sqrt {7}; -2+2· \sqrt {7} \right\} $$
Pero como la función lineal era sólo para los números negativos y el cero, debemos descartar la solución positiva.
Resultando:
$$ S = \left\{ -2-2· \sqrt {7}\right\} $$
Y por otro lado:
$$ x^2 + 2·x - 24 = -x^2 + 4·x ⇒ 2·x^2 - 2·x -24 = 0 $$
Resolviendo por Bháskara llegamos a:
$$ S = \left\{ -3; 4 \right\} $$
Pero como la función cuadrática era sólo para los números positivos debemos descartar la solución negativa.
Resultando:
$$ S = \left\{ 4 \right\} $$
En efecto, las grafico para verificar que sí son las raíces:
Ahora que tenemos las raíces vamos a hacer el estudio del signo: ponemos las raíces de menor a mayor y pensamos.
Luego del punto \( x = 4 \), ¿cómo es el signo de la la función resultante? Pues, ¡es negativo! Por esta razón comenzamos desde la izquierda y ponemos negativo y vamos alternando entre negativo y positivo, cada vez que pasa por una raíz cambia su signo.
¿Cómo sé que es negativo el signo después de dicho punto? Pues veamos, el término principal de la función \( f(x) \) es en todo momento negativo, mientras que el de la función \( t(x) \) es positivo, cuando restamos vamos a tener que \( -x^2 - (x^2) = - 2·x^2 \), pasaría también en el caso de la función lineal, más allá de que mi ejemplo haya sido de la función cuadrática.