|
   |
| Foro Departamento de Matemática Problemas resueltos Función cuadrática |
| Función cuadrática |
|
05-12-2012, 5:22 PM
Post: #1
|
|||
|
|||
|
1) Dada la función \( f(x)= -x^2 + 2·x + 8 \)
a) Graficarla a partir de sus elementos. b) Expresarla en forma canónica y factoreada. 2) Hallar la ecuación de la función que responde al siguiente grafico:  |
|||
 |
|
05-12-2012, 5:27 PM
Post: #2
|
|||
|
|||
|
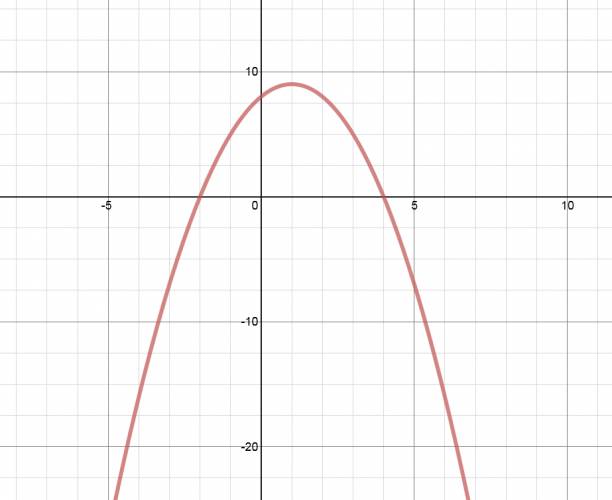
1. Hallamos las raíces de la función: igualándola a 0.
\( -x^2 + 2·x + 8 = 0 \) El conjunto solución de dicha ecuación es: \( S = \left\{ -2, 4\right\} \) El término independiente (8) es la ordenada en el origen: intersección del gráfico con el eje vertical, mientras que las raíces son las intersecciones con el eje horizontal. Como es una función cuadrática su gráfico es una parábola, queda lo siguiente:  Como el coeficiente principal es negativo: tiene concavidad negativa. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
 |
|
05-12-2012, 5:36 PM
Post: #3
|
|||
|
|||
|
b.
Forma factorizada: \( - 1 · (x + 2)·(x - 4) \) Forma canónica: \( - 1 · (x - 1)^2 + 9 \) ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
|
05-12-2012, 5:40 PM
Post: #4
|
|||
|
|||
|
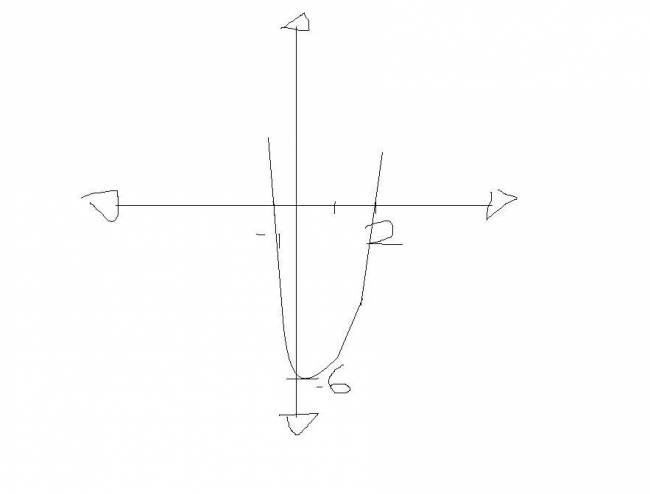
2. El gráfico nos proporcionas sus raíces: \( S = \left\{ -1, 2\right\} \), y también su ordenada en el origen: -6.
Por el teorema del factor tenemos lo siguiente: \(f(x) = a·(x + 1)·(x - 2) \) Y como la ordenada en el origen es 0, tenemos que: \(f(0) = a·(0 + 1)·(0 - 2) = -6 \) \(a·(1)·(-2) = -6 \) \( -2·a = -6 \) \( a = \frac {-6}{-2} = 3 \) Entonces nos queda que: \(f(x) = 3·(x + 1)·(x - 2) \) ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
|
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
| Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
| PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
| Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
| PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |