|
| Foro Departamento de Matemática Problemas resueltos Hallar los vértices de un triángulo conociendo los puntos me |
| Hallar los vértices de un triángulo conociendo los puntos me |
|
20-09-2012, 0:26 AM
Post: #1
|
|||
|
|||
|
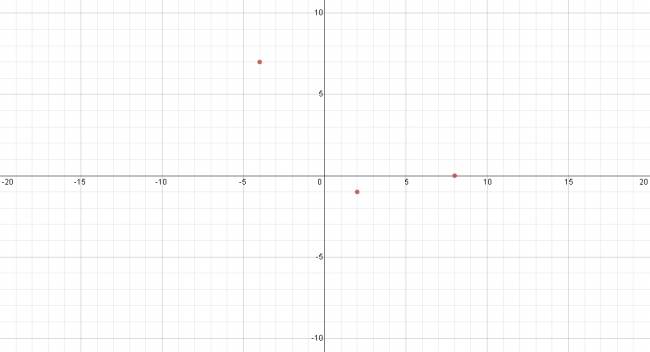
Se quieren hallar los vértices de un triángulos MNP sabiendo que los puntos medios de sus lados son A(8,0); B(-4,7); C(2,-1).
|
|||
|
20-09-2012, 0:27 AM
Post: #2
|
|||
|
|||
|
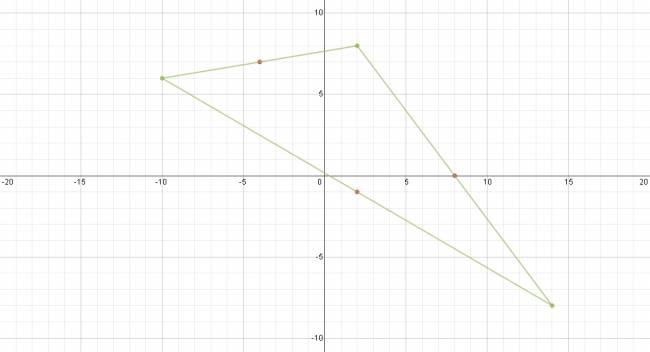
Primero que nada: para tener bien en claro los puntos medios: los graficaré.
Sé que la fórmula para obtener los puntos medios de una coordenada son: $$ Z \left ( \frac {x_{1}+x_{2}}{2}; \frac {y_{1}+y_{2}}{2} \right ) $$ Cuando digo que A(8,0), estoy diciendo que el punto A tiene abscisa 8 y ordenada 0, que en lenguaje matemático sería: \( x=8 \) e \( y=0 \). Esta descomposición la pueda aplicar a todos los puntos y ésto es lo que haré. Como los extremos no los conozco pero sé cuanto da la semisuma de ellos, los igualaré al resultado. Para hallar las abscisas de los puntos M y N, correspondientes al punto medio A: 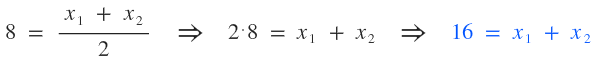 Para hallar las ordenadas de los puntos M y N, correspondientes al punto medio A: 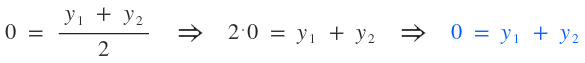 Para hallar las abscisas de los puntos M y P, correspondientes al punto medio B: 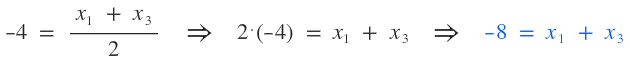 Para hallar las ordenadas de los puntos M y P, correspondientes al punto medio B: 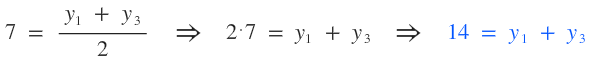 Para hallar las abscisas de los puntos N y P, correspondientes al punto medio C: 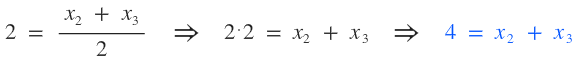 Para hallar las ordenadas de los puntos N y P, correspondientes al punto medio C: 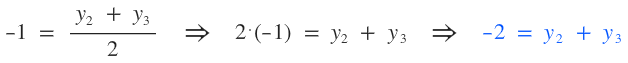 Ahora estableceré un sistema de ecuación con las abscisas: 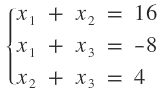 Ahora sólo hace falta resolver. Resolver un sistema de 3x3 es bastante largo, así que este paso me lo saltearé y pondré sólo las raíces (cualquier duda puedes preguntar): 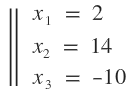 Ahora estableceré otro sistema de ecuaciones con las ordenadas: 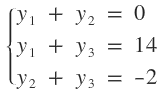 Cuyas raíces son: 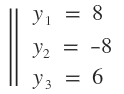 Ahora estableceré las siguientes relaciones: 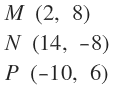 Ahora para que se vea que llegamos a lo que queríamos: En esta última captura me he tomado la molestia representar el triángulo (verde) para que se vean bien los puntos medios.  ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
29-09-2013, 8:19 PM
Post: #3
|
|||
|
|||
|
oyes disculpa cual es el sistema de tres por tres te agradeceria mucho
|
|||
|
02-10-2013, 2:53 AM
Post: #4
|
|||
|
|||
|
Cita (samuelsoto) oyes disculpa cual es el sistema de tres por tres te agradeceria mucho Al no tratarse de sistemas completos (donde las tres ecuaciones presentan las tres variables), aplicaré una combinación de los métodos de igualación y reducción; es lo más rápido que se me ocurre en el momento. · Para hallar las abscisas: $$ \begin{cases} x_{1} + x_{2} = 16 \\ x_{1} + x_{3} = -8 \\ x_{2} + x_{3} = 4 \end{cases} $$ Despejaré \( x_{1} \) en las primeras dos ecuaciones y las igualaré. $$ x_{1} + x_{2} = 16 ⇒ x_{1} = 16 - x_{2} $$ $$ x_{1} + x_{3} = -8 ⇒ x_{1} = -8 - x_{3} $$ $$ ⇒ 16 - x_{2} = -8 - x_{3} ⇒ x_{2} - x_{3} = 24 $$ Formo un sistema de 2x2 con la ecuación a la que hemos llegado y la última del sistema de ecuaciones. $$ \begin{cases} x_{2} - x_{3} = 24 \\ x_{2} + x_{3} = 4 \end{cases} $$ Este sistema lo resolveré por reducción. Si sumamos las dos ecuaciones, nos resultará la siguiente ecuaciones lineal de una variable: $$ 2·x_{2} = 28 ⇒ x_{2} = 14 $$ Ahora sustituyo el valor conocido en la primera ecuación del sistema problema: $$ x_{1} + x_{2} = 16 ⇒ x_{1} + 14 = 16 ⇒ x_{1} = 2 $$ Ahora sustituyo el valor conocido en la última ecuación del sistema problema: $$ x_{2} + x_{3} = 4 ⇒ 14 + x_{3} = 4 ⇒ x_{3} = -10 $$ La solución del sistema será: $$ S = \left\{ 2, 14, -10 \right\} $$ Espero haberte ayudado, y cualquier otra duda, estoy a las órdenes.  Un saludo. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |