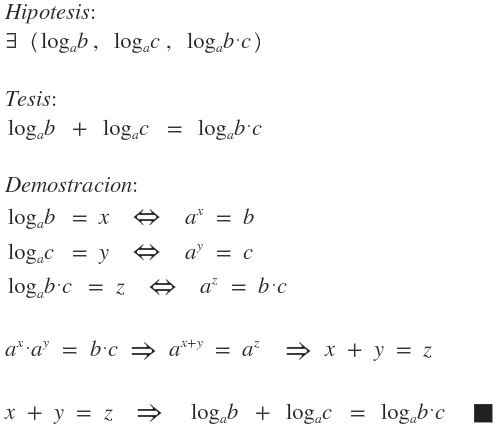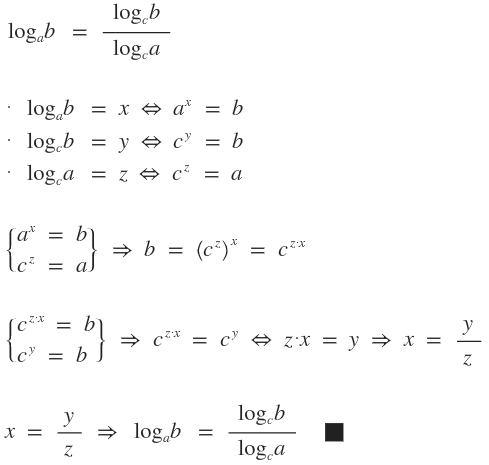|
| Foro Departamento de Matemática Teóricos Logaritmo |
| Logaritmo |
|
27-10-2012, 8:57 PM
Post: #1
|
|||
|
|||
|
Definición:
Logaritmo de un número, en una base determinada, es el exponente al cual hay que elevar la base para obtener dicho número. 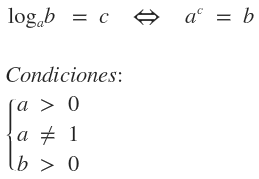 Diferencia entre log y ln: log ⇒ es el logaritmo en base 10 de un número; fue descubierto por Henry Briggs. ln ⇒ es el logaritmo natural o en base \( e \) de un número; fue descubierto por John Napier en 1614 (ln significa logatirmo neperiano). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
27-10-2012, 9:07 PM
Post: #2
|
|||
|
|||
|
Propiedades:
· Suma de logaritmos: $$ \log_{a} b + \log_{a} c = \log_{a} (b·c) $$ · Resta de logaritmos: $$ \log_{a} b + \log_{a} c = \log_{a} (\frac {a}{b}) $$ · Potencia de logaritmos: $$ \log_{a} b^{n} = n·\log_{a} b $$ · Radicación de logaritmos: $$ \log_{a} \sqrt [n]{b} = \frac {1}{n}·\log_{a} b $$ · Opuesto de un logaritmo: $$ -\log_{a} b = \log_{a} (\frac {1}{a}) $$ · Teorema de cambio de base: $$ \log_{a} b = \frac {\log_{c} b}{\log_{c} a} $$ · Logaritmo de base igual al logaritmando: $$ \log_a a = 1 $$ · Logaritmo de logaritmando uno: $$ \log_a 1 = 0 $$ · Exponente de logaritmando: $$ \log_{a^{n}} b^{m} = \frac {m}{n}· \log_{a} b $$ · Inverso de un logaritmo: $$ \log_{a} b = \frac {1}{\log_{b} a} $$ · Exponente de logaritmo: $$ a^{\log_{a} k} = k $$ · Propiedad: $$ \log_{a} \frac {1}{b} = \log_{\frac {1}{a}} a $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
02-11-2012, 8:47 PM
Post: #3
|
|||
|
|||
|
Ecuaciones logarítmicas:
Resolución por calculadora científica: Supongamos que se quiere resolver la ecuación \( 3^x = 27 \) por calculadora científica: $$ 3^x = 27 \Leftrightarrow x = log_{3} 27 \Leftrightarrow x = \frac{log_{10} 27}{log_{10} 3} = 3 $$ Dominio de una ecuación logarítmica: Por definición de logaritmo b es un número positivo. Por lo que se estudia que cada valor de b donde hay una variable sea positivo, de lo contrario no hay solución. Se hace un estudio del signo para cada logaritmando por separado, planteándose una inecuación, de que el logaritmando debe ser mayor que cero, esto se hace a todos los logaritmandos, al final, se buscan todas las partes en que las inecuaciones sean positivas al mismo tiempo y este es el dominio. · Ver ejemplo A tener en cuenta: Muchos programas son capaces de resolver ecuaciones logarítmicas, pero no de hacer el dominio, por lo que tienen raíces que no cumplen las condiciones de existencia. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
24-11-2012, 8:54 PM
Post: #4
|
|||
|
|||
|
Número e:
El número \( e \), también conocido como número de Euler, es la base de los logaritmos neperianos. Este número es irracional, por lo que sus decimales (número después de la coma) son infinitos y no se repiten (no son periódicos). ¿Cómo calcularlo? Hay diversas formas de calcularlo, algunas de ellas son: Por medio de límite: $$ \lim_{x \to{+}\infty} \left({1+\displaystyle\frac{1}{n}}\right)^n = e$$ Utilizando sumatoria: $$ \sum_{n=0}^\infty \frac{1}{n!} = e $$ Aproximación: $$ e \approx 2,71828 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
06-12-2012, 6:49 PM
Post: #5
|
|||
|
|||
|
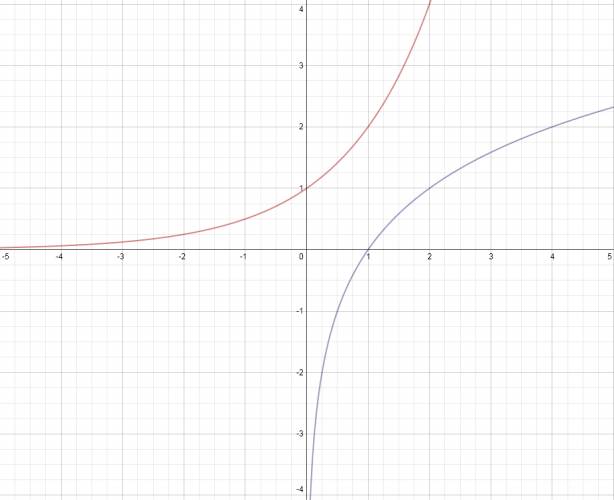
Función logarítmica:
$$ f(x) = 2^x $$ $$ t(x) = log_{2} x $$ La función \( f \) es una función exponencial, mientras que la función \( t \) es una función logarítmica. Se puede observar un eje de simetría entre ellas en \( y = x \). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |