27-10-2012, 8:57 PM
Definición:
Logaritmo de un número, en una base determinada, es el exponente al cual hay que elevar la base para obtener dicho número.
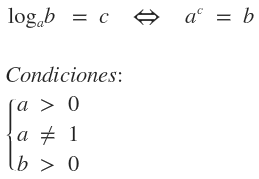
Diferencia entre log y ln:
log ⇒ es el logaritmo en base 10 de un número; fue descubierto por Henry Briggs.
ln ⇒ es el logaritmo natural o en base \( e \) de un número; fue descubierto por John Napier en 1614 (ln significa logatirmo neperiano).
Logaritmo de un número, en una base determinada, es el exponente al cual hay que elevar la base para obtener dicho número.
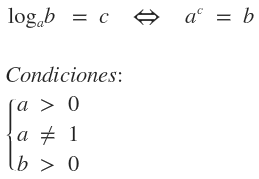
Diferencia entre log y ln:
log ⇒ es el logaritmo en base 10 de un número; fue descubierto por Henry Briggs.
ln ⇒ es el logaritmo natural o en base \( e \) de un número; fue descubierto por John Napier en 1614 (ln significa logatirmo neperiano).