|
| Foro Departamento de Matemática Teóricos Geometría analítica en el plano cartesiano |
| Geometría analítica en el plano cartesiano |
|
25-07-2013, 4:13 AM
Post: #1
|
|||
|
|||
|
Geometría analítica en el plano cartesiano
La geometría analítica es la rama de la matemática que se dedica al estudio de figuras geométricas aplicando técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas (en nuestro caso el cartesiano). ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 4:15 AM
Post: #2
|
|||
|
|||
|
El plano cartesiano
El plano cartesiano fue el primer plano de representación de coordenadas. Fue ideado por el matemático francés René Descartes que usó el seudónimo de Cartesius. Descartes no sólo ideó el plano de coordenadas que lleva su nombre, sino que fue quien sentó las bases de la geometría analítica. El plano de ejes cartesianos, es el formado por dos rectas perpendiculares. · La recta vertical recibe el nombre de eje de las ordenadas o eje \( O \vec y \). · La recta horizontal recibe el nombre de eje de las abscisas o eje \( O \vec x \). · La intersección de las dos rectas es el punto \( O (0, 0) \) llamado origen de coordenadas. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 4:17 AM
Post: #3
|
|||
|
|||
|
El punto
Notación: \( P (x_{1}, y_{1}) \) · Distancia entre dos puntos: Dados dos puntos \( A (x_{A}, y_{A}) \) y \( B (x_{B}, y_{B}) \), la distancia entre ellos está dada por la fórmula: $$ d(A, B) = \sqrt {(x_{A}-x_{B})^2 + (y_{A}-y_{B})^2} $$ · Punto del medio del segmento formado por dos puntos: El punto medio del segmento \( \overline {AB} \), formado por los puntos \( A(x_{A},y_{A}) \) y \( B(x_{B},y_{B}) \), está dado de la siguiente forma: $$ M_{\overline {AB}} = \left ( \frac {x_{A} + x_{B}}{2}; \frac {y_{A} + y_{B}}{2} \right ) $$ · Distancia de un punto a una recta: La distancia de un punto a una recta, es la distancia más corta entre amos, o sea, es la medida del segmento perpendicular a la recta, cuyo uno de sus vértices es la propia recta y el otro, es el punto. Pudiéndose calcular como: sea el punto \( A(x_{A}, y_{A}) \) y la recta en su forma general: \( ( r ) a·x+b·y+c = 0 \), la distancia de \( A \) a \( ( r ) \) se puede calcular a través de la fórmula: $$ d(A,r) = \frac {|a·x_{A}+b·y_{A}+c|}{\sqrt {a^2+b^2}} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 4:27 AM
Post: #4
|
|||
|
|||
|
Recta
Toda recta (en geometría analítica) es una ecuación en dos variables, donde ambas variables \( x \) e \( y \) son de primer grado. Una recta tiene infinitas ecuaciones que la identifican. · Tipos de ecuaciones de la recta: · Rectas paralelas: · Rectas perpendiculares: · Intersección de dos rectas: · Inecuación de una recta: · Familia de rectas: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 4:34 AM
Post: #5
|
|||
|
|||
|
Secciones cónicas
Definición de cónica: Se llama cónica al lugar geométrico de los puntos del plano cuyas coordenadas cartesianas verifican una ecuación de segundo grado en dos variables. Absolutamente todas las cónicas tienen la forma: $$ a·x^2 + b·y^2 + c·x·y + d·x + e·y + f = 0 $$ Donde los coeficientes: \( a,b,c,d,e,f \) son números reales. Las cónicas son cuatro, y resultan de la intersección entre un cono y un plano:  Ecuación de una figura: · Propiedades fundamentales: 1. Todo punto que pertenezca a la figura, sus coordenadas verifican su ecuación. 2. Todo punto cuyas coordenadas verifican la ecuación, pertenecen a la figura. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 6:27 PM
Post: #6
|
|||
|
|||
|
Circunferencia
Toda circunferencia (en geometría analítica) es una ecuación de dos variables, donde ambas variables \( x \) e \( y \) son de segundo grado, con posibilidad de tener también variables \( x \) e \( y \) de primer grado. Definición: Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro, una media constante llamada radio. Por nuestra definición de circunferencia (de aquí en más cfa), podemos ver que una cfa no es lo mismo que un círculo, ya que el círculo no es otra cosa que la región del plano delimitada por una circunferencia y que posee un área definida. Cita   La imagen izquierda es una cfa, mientras que la derecha es un círculo. · Tipos de ecuaciones de la cfa: · Cfa que pasa por tres puntos: · Intersección de una recta con una cfa: · Inecuación de una cfa: · Recta tangente a una cfa en un punto: · Familia de cfas: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 6:30 PM
Post: #7
|
|||
|
|||
|
Elipse
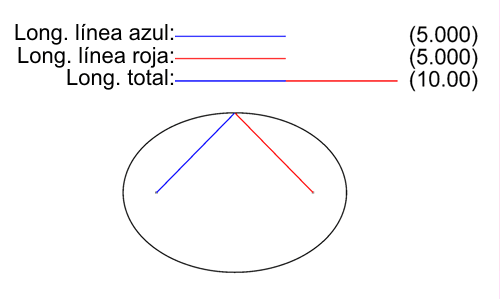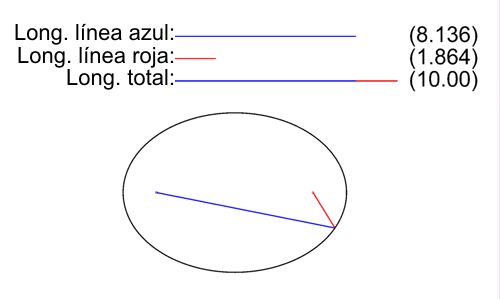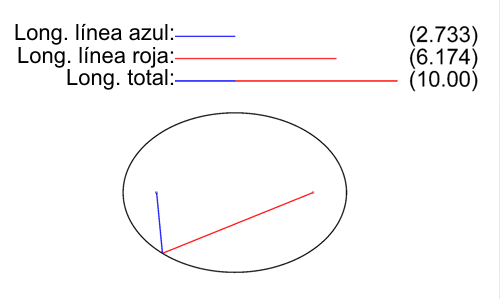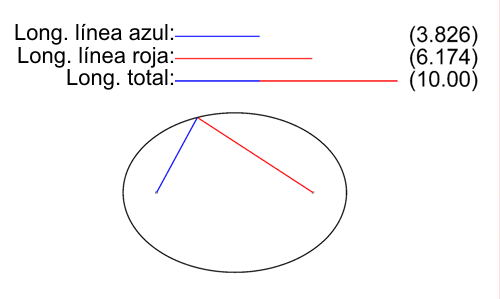 Notación: De aquí en más denotaré con \( \mathcal{E} \) a una elipse. Definición: Dados dos puntos F y F' (focos) y un número real positivo \( 2·a / 2·a > d(F,F') \), se llama elipse, al lugar geométrico de los puntos del plano, cuya suma de distancias a F y F' sea siempre constante e igual a \( 2·a \). Todo punto P que pertenezca a la elipse debe cumplir que: $$ ∀P∈ \mathcal{E} ⇔ d(P,F)+d(P,F') = 2·a / 2·a > d(F,F') $$ Elementos de una elipse: · Focos: F y F' \( / d(F,F') = 2·c \) · Número real positivo \( 2·a∈ℝ^{+} / 2·a > 2·c ⇒ a > c \) · Ejes de simetría: :: Eje focal: la recta FF'. :: Eje transverso: mediatriz de FF'. · Centro de simetría: O, punto medio de FF'. · Vértices: :: A y A' los cuales pertenecen al eje focal. :: B y B' los cuales pertenecen al eje transverso. · Longitud del segmento AA': \( d(A,A') = 2·a \) 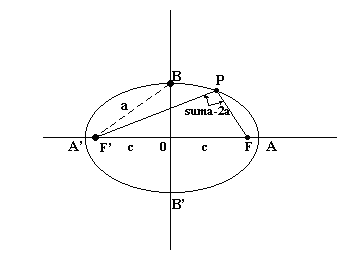 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 6:30 PM
Post: #8
|
|||
|
|||
|
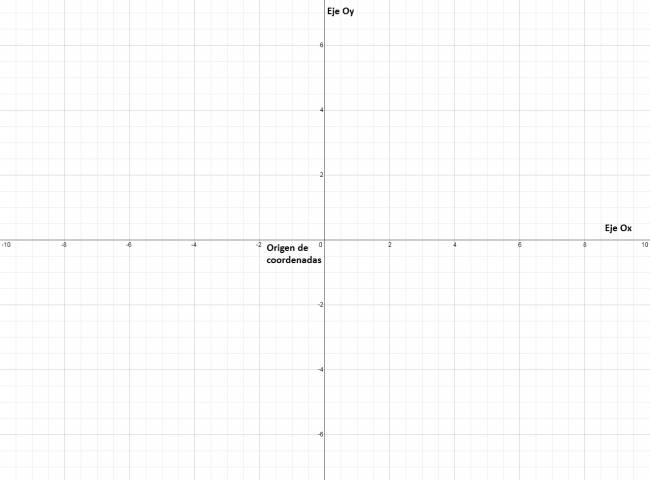
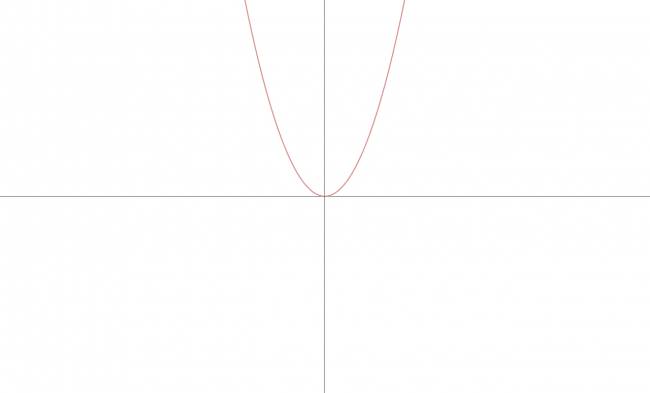
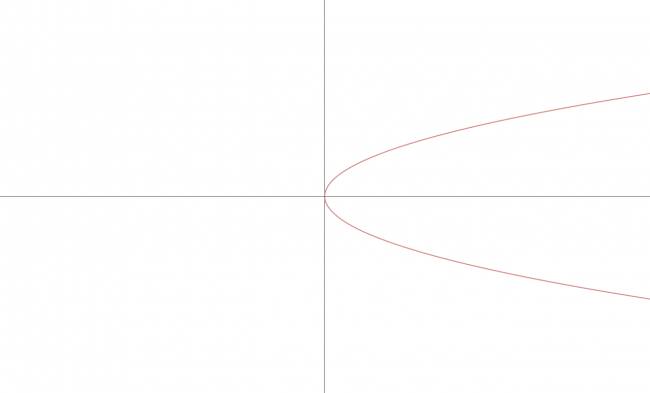
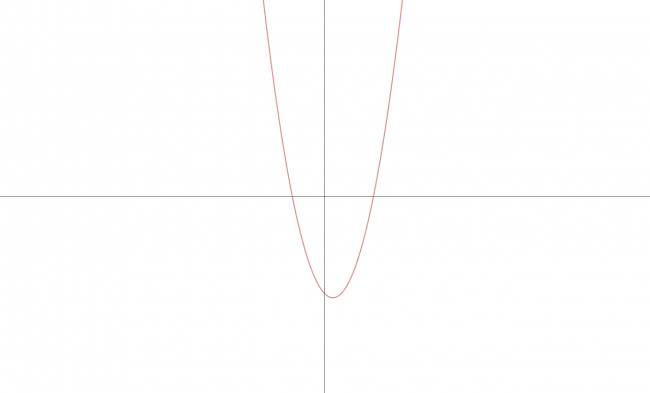
Parábola
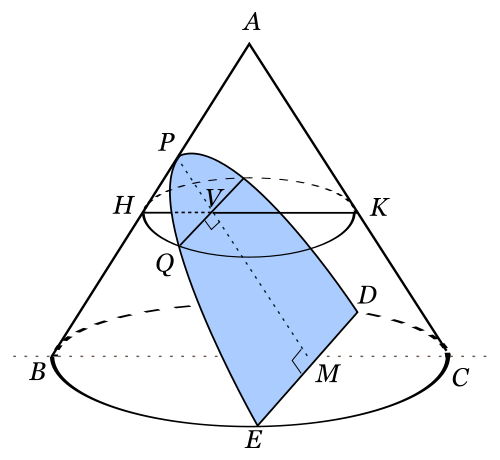 Notación: De aquí en más denotaré con \( \mathcal{P} \) a una parábola. Definición: Dados un punto \( F \) (foco) y una recta \( d \) (directriz) tal que \( F∉d \), se llama parábola al lugar geométrico de los puntos del plano que equidistan del foco y de la directriz. Todo punto \( M \) que pertenezca a la parábola debe cumplir que: $$ M∈\mathcal{P} ⇔ d(M,F) = d(M,d) $$ Elementos de una parábola: · Foco: \( F \) · Directriz: \( d / F∉d \) · Parámetro: \( p = d(F,d), p∈ℝ^{+} \) · Vértice: \( v \), es el punto medio del segmento de la perpendicular desde \( F \) hasta \( d \). · Eje focal: es la recta perpendicular a la directriz que pasa por el foco. Cita 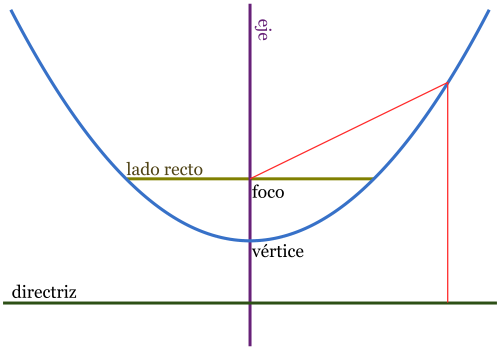 Casos de posibles parábolas: · Primer caso: $$ y=a·x^2, a≠0 $$ Elementos de la parábola del primer caso: · Vértice: $$ V (0,0) $$ · Foco: $$ F \left ( 0, \frac {1}{4·a} \right ) $$ · Directriz: $$ (d) y = - \frac {1}{4·a} $$ · Segunda caso: $$ x = a·y^2, a≠0 $$ Elementos de la parábola del segundo caso: · Vértice: $$ V (0,0) $$ · Foco: $$ F \left ( \frac {1}{4·a}, 0 \right ) $$ · Directriz: $$ (d) x = - \frac {1}{4·a} $$ · Tercer caso: $$ y = a·x^2 + b·x + c, a≠0 $$ Elementos de la parábola del tercer caso: · Vértice: $$ V \left ( \frac {-b}{2·a}, \frac {4·a·c-b^2}{4·a} \right ) $$ · Foco: $$ F \left ( \frac {-b}{2·a}, \frac {4·a·c-b^2+1}{4·a} \right ) $$ · Directriz: $$ (d) y = \frac {4·a·c-b^2-1}{4·a} $$ · Cuarto caso: $$ x = a·y^2 + b·y + c, a≠0 $$ Elementos de la parábola del tercer caso: · Vértice: $$ V \left ( \frac {4·a·c-b^2}{4·a}, \frac {-b}{2·a} \right ) $$ · Foco: $$ F \left ( \frac {4·a·c-b^2+1}{4·a}, \frac {-b}{2·a} \right ) $$ · Directriz: $$ (d) x = \frac {4·a·c-b^2-1}{4·a} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
25-07-2013, 6:39 PM
Post: #9
|
|||
|
|||
|
Hipérbola
Notación: De aquí en más denotaré con \( \mathcal{H} \) a una elipse. Definición: Dados dos puntos F y F' (focos) y un número real positivo \( 2·a / 2·a < d(F,F') \), se llama hipérbola al lugar geométrico de los puntos del plano, cuya resta de distancias, en valor absoluto, a F y F' sea constante e igual a \( 2·a \). Todo punto P que pertenezca a la hipérbola debe cumplir que: $$ ∀P ∈ \mathcal{H} ⇔ |d(P,F) - d(P,F')| = 2·a $$ Elementos de la hipérbola: · Focos: F y F' \( / d(F,F') = 2·c \) · Número real positivo: \( 2·a \) · Ejes de simetría: :: Eje focal: la recta FF'. :: Eje transverso: la mediatriz de FF'. · Centro de simetría: O, punto medio de FF'. · Vértices: A y A' tales que pertenecen al eje focal. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |