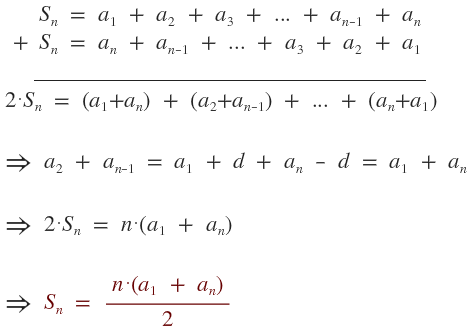|
| Foro Departamento de Matemática Teóricos Sucesiones |
| Sucesiones |
|
10-05-2013, 2:20 AM
Post: #1
|
|||
|
|||
|
Definición:
Una sucesión es una función cuyo dominio es el conjunto de los números naturales o a partir de un número natural dado. $$ f: ℕ → ℝ $$ Observaciones: · Lo importante es no considerar un subconjunto de números naturales que esté acotado superiormente como dominio. · El codominio no debe ser necesariamente un subconjunto de números naturales, puede ser uno de números reales. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
10-05-2013, 2:22 AM
Post: #2
|
|||
|
|||
|
Sucesiones definidas por recurrencia:
Llevan este nombre porque recurren al término anterior. $$ p.r \begin{cases} a_{1} \\ a_{n} = 2·a_{n-1} + 1 \end{cases} $$ Ejemplo: Sucesión de Fibonacci: Es una progresión aritmética por recurrencia, donde el término siguiente se halla a partir de la suma de los dos anteriores. $$ \mbox{Sucesión de Fibonacci } \begin{cases} a_{1} = 0 \\ a_{2} = 1 \\ a_{n} = a_{n-1} + a_{n-2} \end{cases} $$ Primeros términos de la sucesión: 1, 1, 2, 3, 5, 8, 13, ... ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
10-05-2013, 2:22 AM
Post: #3
|
|||
|
|||
|
Progresiones aritméticas:
Definición: Es una sucesión definida por recurrencia en la que un término se encuentra a partir del anterior sumándole una constante, ésta constante se llama diferencia (denotada como \( d \)). $$ p.a \begin{cases} a_{1} \\ a_{n} = a_{n-1} + d \end{cases} $$ Ejemplo: Sea la sucesión aritmética: $$ p.a_{1} \begin{cases} a_{1} = 2 \\ a_{n} = a_{n-1} + 5 \end{cases} $$ Primeros términos de la sucesión: 2, 7, 12, 17, 22, ... Suma de los primeros \( n \) términos de una progresión aritmética: $$ S_{n} = \frac {n·(a_{1} + a_{n})}{2} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
10-05-2013, 2:23 AM
Post: #4
|
|||
|
|||
|
Progresiones geométricas:
Definición: Es una sucesión definida por recurrencia en la que un término se encuentra a partir del anterior multiplicándole una constante, ésta constante se llama razón (denotada como \( q \)). $$ p.g \begin{cases} a_{1} \\ a_{n} = a_{1}·q^{n-1} \end{cases} $$ Ejemplo: Sea la sucesión geométrica: $$ p.g_{1} \begin{cases} a_{1} = 3 \\ a_{n} = a_{1}·2^{n-1} \end{cases} $$ Primeros términos de la sucesión: 3, 6, 12, 24, 48, ... Suma de los primeros \( n \) términos de una progresión geométrica: $$ S_{n} = \frac {a_{1}-a_{n}·q}{1-q} $$ $$ S_{n} = \frac {a_{1}·(1-q^n)}{1-q} $$ Suma de los infinitos términos de una progresión geométrica: Sólo se cumple para progresiones geométricas cuya razón en valor absoluto es menor que la unidad \( ( |q|<1 ) \). En el caso que la progresión geométrica tenga una razón mayor que la unidad, la suma de la la progresión jamás será un número, sino que será infinito. En este último caso, no nos importará esta fórmula porque ya sabremos que el resultado de la suma es infinito. $$ S_{∞} = \frac {a_{1}}{1-q} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
10-05-2013, 2:24 AM
Post: #5
|
|||
|
|||
|
Límite de una sucesión:
El límite de una sucesión es el o los valores a los que tiende la sucesión al tomar valores cada vez mayores. $$ \lim_{n \to +∞} a_{n} $$ Clasificación: · Convergente: cuando tiende a un número · Divergente: cuando tiende a más infinito o a menos infinito. · Oscilante: cuando tienden a más de un número. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |