| Foro Departamento de Matemática Teóricos Graficar: funciones, ecuaciones, inecuaciones, ... |
| Graficar: funciones, ecuaciones, inecuaciones, ... |
|
12-04-2013, 2:49 AM
Post: #1
|
|||
|
|||
|
En este tema intentaré explicar los métodos más sencillos para graficar funciones, ecuaciones, inecuaciones, y otros tipos de expresiones matemáticas.
¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-04-2013, 2:51 AM
Post: #2
|
|||
|
|||
|
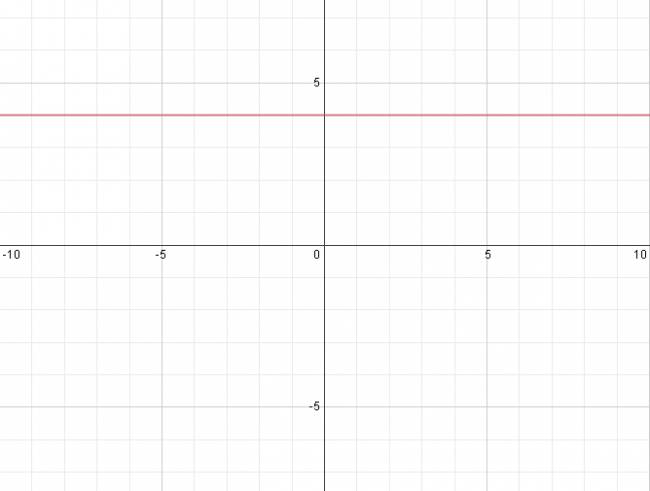
Función constante:
Se traza una recta horizontal (paralela al eje \( x \)) que pase por el valor de la función en el eje \( y \). Ejemplo: $$ f(x) = 4 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-04-2013, 2:54 AM
Post: #3
|
|||
|
|||
|
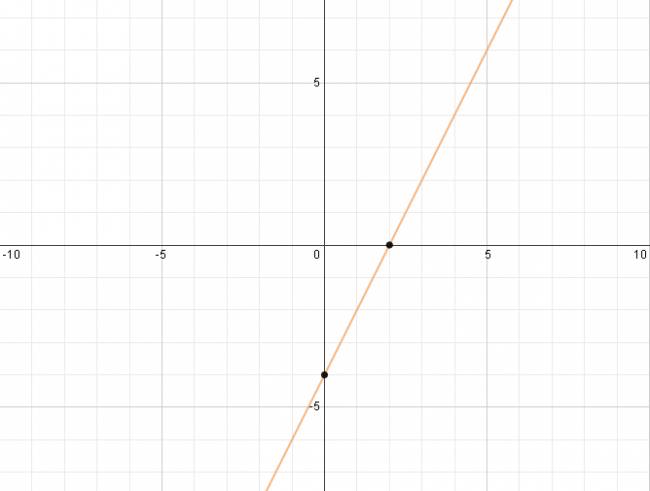
Función de primer grado o lineal:
Este tipo de expresiones tienen como representación gráfica una recta que nunca es paralela, NUNCA. Sabemos que por dos puntos sólo puede pasar una única recta, por lo que calculamos la raíz y la ordenada en el origen de la función y graficamos los dos puntos, luego de esto trazamos la única recta que pasa por estos. $$ f(x) = 2·x - 4 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-04-2013, 2:58 AM
Post: #4
|
|||
|
|||
|
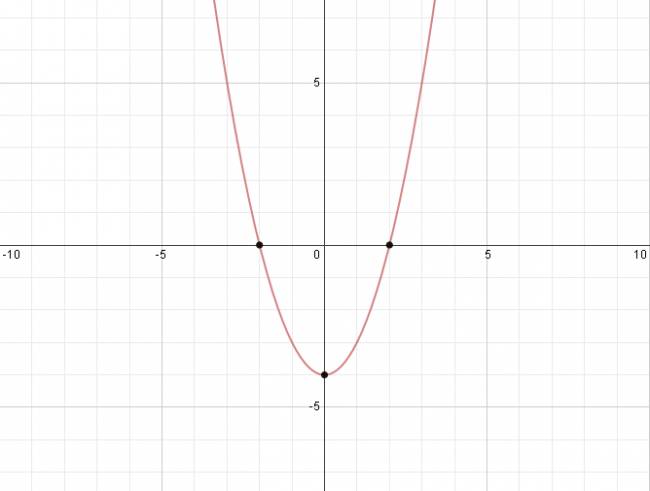
Función de segundo grado o cuadrática:
Debemos hallar las raíces, la ordenada en el origen y el vértice. Luego de haber calculado todo esto graficamos los puntos y trazamos la mejor parábola que nos salga que pase por estos puntos. $$ f(x) = x^2 - 4 $$ En este ejemplo la ordenada en el origen coincide con el vértice, tenerlo en cuenta. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-04-2013, 3:05 AM
Post: #5
|
|||
|
|||
|
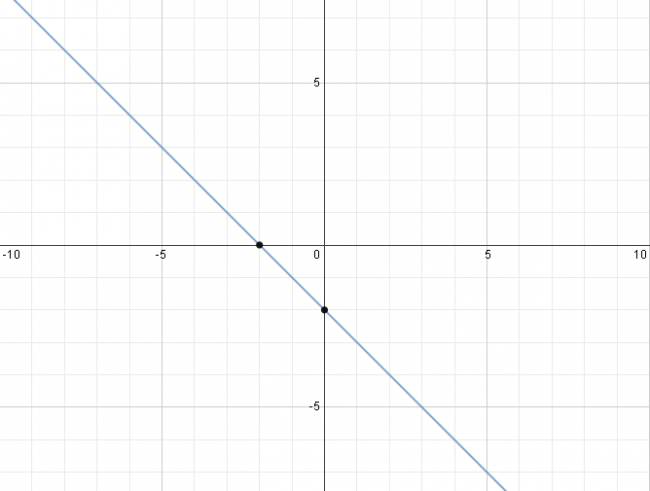
Recta en el plano (dos variables):
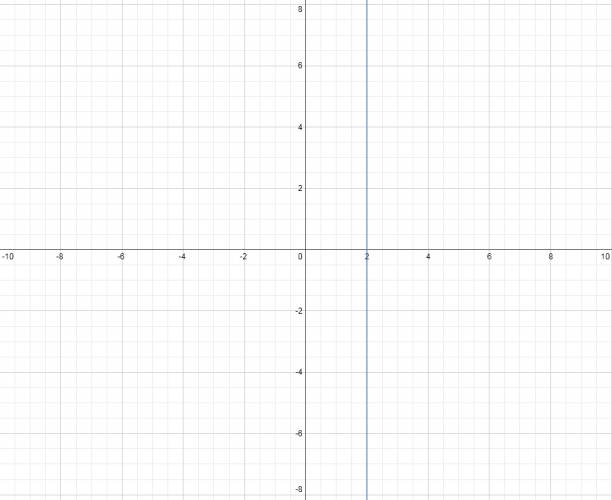
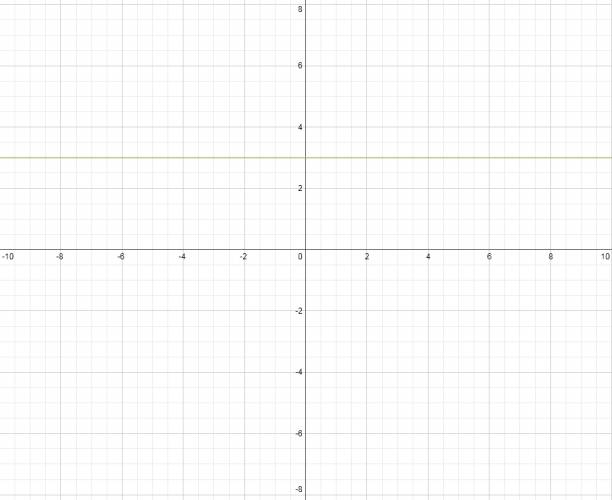
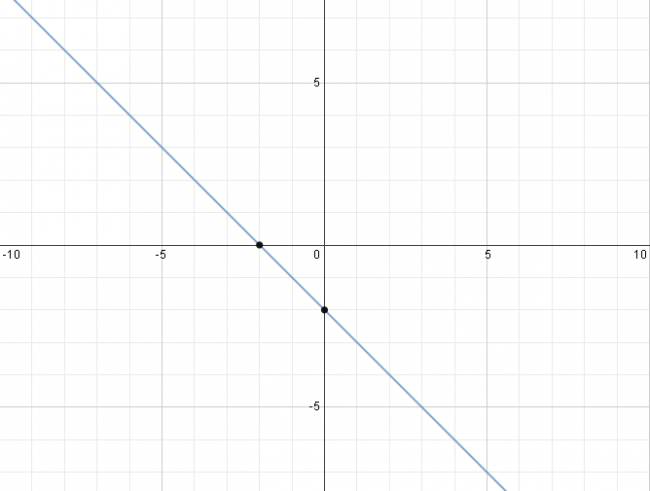
· Para las ecuaciones del tipo \( a·x + b·y + c = 0 \) donde \( a \) y \( b \) no son nulos: Pasos: 1. Se despeja a 0. 2. Se sustituye \( x = 0 \) y se resuelve, llegando a un valor de \( y \), lo cual se puede interpretar como un punto \( (0,y) \). 3. Se sustituye \( y = 0 \) y se resuelve, llegando a un valor de \( x \), lo cual se puede interpretar como un punto \( (x,0) \). 4. Se grafican los puntos. 5. Se traza la única recta que pasa por esos puntos. Ejemplo: Code Graficar la recta: \( 2·x + 2·y = -4 \) $$ 2·x + 2·y = -4 ⇒ 2·x + 2·y + 4 = 0 $$ $$ 2·x + 2·y + 4 = 0 ⇒ 2·y = -4 ⇒ y = -2 ⇒ (0,-2) $$ $$ 2·x + 2·y + 4 = 0 ⇒ 2·x = -4 ⇒ x = -2 ⇒ (-2,0) $$ Graficamos los puntos y trazamos la recta que pasa por ellos. · Para las ecuaciones de la recta del tipo \( x = a \): \( a \) es un número real cualquiera. Se dice que esta recta no tiene pendiente. Es una recta vertical, paralela al eje \( y \) que corta el eje de las \( x \) en \( x = a \), muy obvio, ¿no? Ejemplo: $$ x = 2 $$ · Para las ecuaciones de la recta del tipo \( y = b \): \( b \) es un número real cualquiera. Se dice que esta recta tiene pendiente nula. Es una recta horizontal, paralela al eje \( x \) que corta el eje de las \( y \) en \( y = b \), muy obvio, ¿no? Ejemplo: $$ y = 3 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
12-04-2013, 3:11 AM
Post: #6
|
|||
|
|||
|
Inecuación en el plano (dos variables):
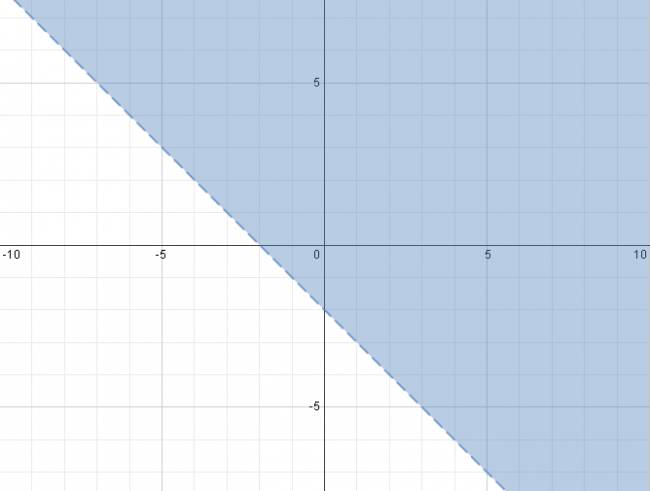
Pasos: 1. Se desiguala a 0. 2. Se iguala a 0. 3. Se sustituye \( x = 0 \) y se resuelve, llegando a un valor de \( y \), lo cual se puede interpretar como un punto \( (0,y) \). 4. Se sustituye \( y = 0 \) y se resuelve, llegando a un valor de \( x \), lo cual se puede interpretar como un punto \( (x,0) \). 5. Se grafican los puntos. 6. Se traza la única recta que pasa por esos puntos. 7. Se toma un punto testigo que no pertenezca a la recta (total, hay infinitos) y se sustituye en la ecuación, el semiplano al que pertenezca el punto tendrá el mismo signo que el valor resultante del valor numérico. Ejemplo: Code Graficar la recta: \( 2·x + 2·y > -4 \) $$ 2·x + 2·y > -4 ⇒ 2·x + 2·y + 4 > 0 ⇒ 2·x + 2·y + 4 = 0 $$ $$ 2·x + 2·y + 4 = 0 ⇒ 2·y = -4 ⇒ y = -2 ⇒ (0,-2) $$ $$ 2·x + 2·y + 4 = 0 ⇒ 2·x = -4 ⇒ x = -2 ⇒ (-2,0) $$ Graficamos los puntos y trazamos la recta que pasa por ellos. Ahora tomamos un punto testigo que no pertenece a la ecuación, por ejemplo el origen \( (0,0) \). $$ 2·x + 2·y + 4 ⇒ 2·0 + 2·0 + 4 = +4 $$ Esto significa que la parte de arriba de la recta es positiva. A mí en el ejercicio me piden que marque la parte positiva, por lo que marcaré el semiplano al que pertenece el origen: Quote Llamamos plano a la totalidad del espacio (lugar geométrico) donde trabajamos. Una recta lo divide en dos partes, cada una de ellas se conoce como semiplano. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-04-2013, 0:04 AM
Post: #7
|
|||
|
|||
|
Inecuación de valor absoluto en el plano (dos variables):
Se resuelve formando sistemas de ecuaciones. Se deberán formar el doble de sistemas de ecuaciones que de expresiones que estén dentro de las barras de valor absoluto. Se aplica la definición de valor absoluto para la expresión que se encuentra dentro de las barras de valor absoluto. Y se trabaja con el resto de la expresión. Bueno, para que se entienda bien esto, recomiendo ver el ejemplo. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-04-2013, 0:04 AM
Post: #8
|
|||
|
|||
|
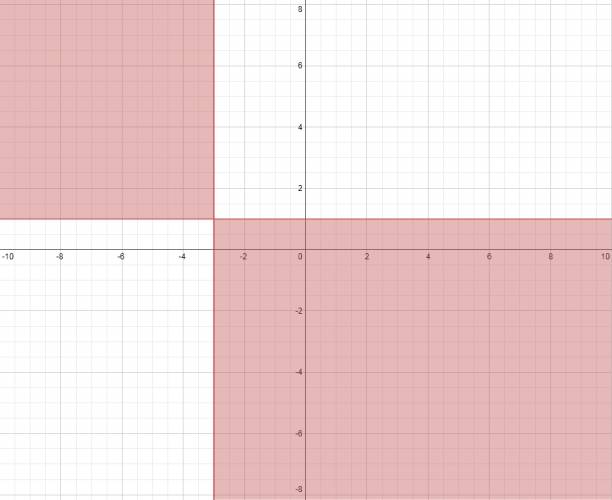
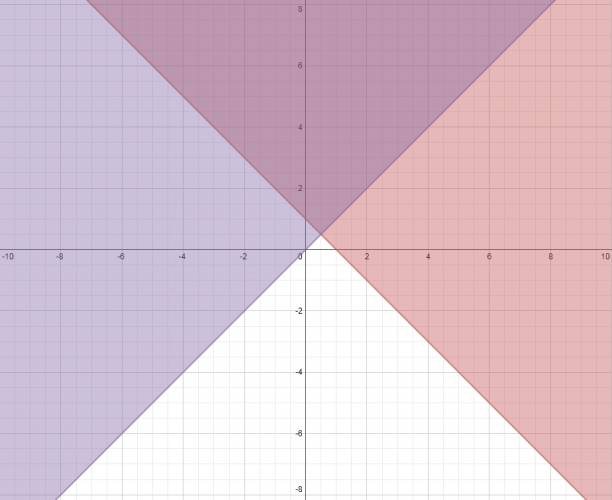
Inecuación de producto de rectas en el plano (dos variables):
1. Se grafica cada recta del producto por separado. 2. Averiguamos en qué semiplano es positiva y negativa cada una de ellas. 3. Nos basamos en la ley de los signos, si se nos pide: Quote Que el producto sea negativo es porque ambas rectas deben tener signo opuesto. Que el producto sea positivo es porque ambas rectas deben tener el mismo signo. Si se pide que también sea 0: las rectas siempre serán solución. Ejemplo: $$ (x+3)·(x-1) ≤ 0 $$ · Trazamos la recta: \( r) x + 3 = 0 \). Que es positiva a la derecha de esta. · Trazamos la recta: \( s) y - 1 = 0 \). Que es positiva arriba de esta. La solución es la parte marcada en rojo, las rectas están incluidas porque me piden negativo o cero. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
13-04-2013, 0:08 AM
Post: #9
|
|||
|
|||
|
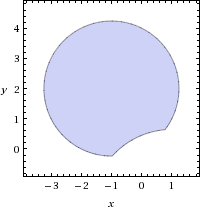
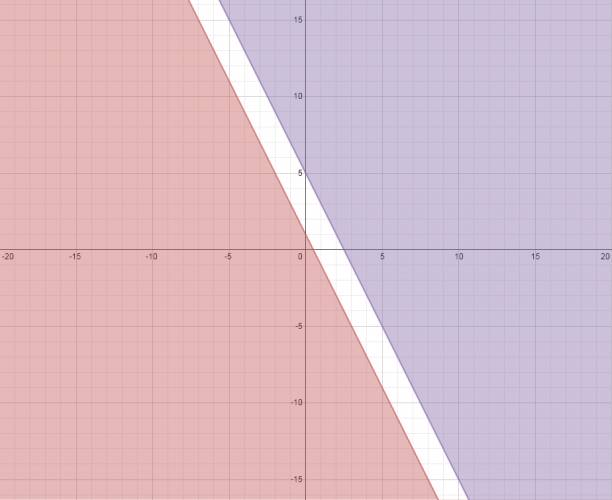
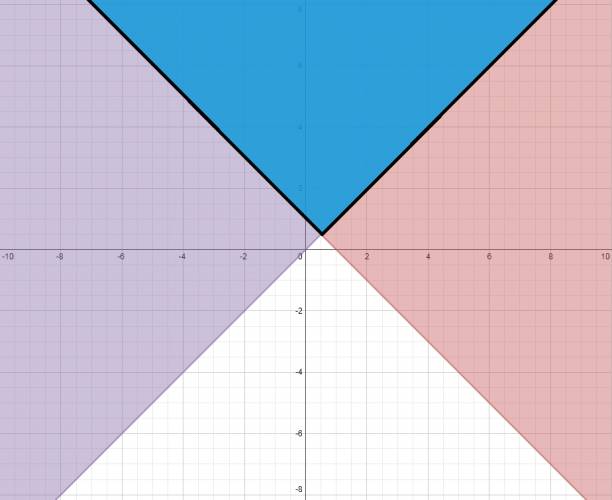
Sistema de inecuaciones en el plano (dos variables):
Un sistema de inecuaciones es aquel formado por al menos dos inecuaciones. Decimos que la intersección del conjunto solución de ambas inecuaciones da el conjunto solución del sistema, o sea, buscamos la solución común a las dos inecuaciones. Por lo que si tengo un sistema de inecuaciones formado por al menos dos inecuaciones que al menos dos de ellas no se intersecten entre sí en ningún momento, puedo afirmar que el conjunto solución de dicho sistema es vacío. Pasos: 1. Se grafican ambas inecuaciones por separado en un mismo gráfico. 2. La solución es la intersección de la solución de ambas inecuaciones. Ejemplo: $$ \begin{cases} x + y - 1 ≥ 0 \\ y - x ≥ 0 \end{cases} $$ Grafico ambas inecuaciones: Marco el conjunto solución: La solución es la parte marcada en azul y las partes negras sobre las rectas. ¿Cómo se escribe el conjunto solución? Bueno, simplemente lo podés marcar y aclarar bien qué parte pintada considerás que es el conjunto solución. No existe ninguna notación matemática específica para esto. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
03-06-2013, 1:35 AM
Post: #10
|
|||
|
|||
|
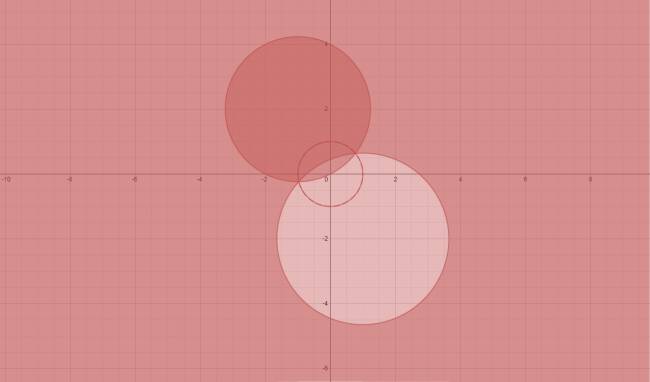
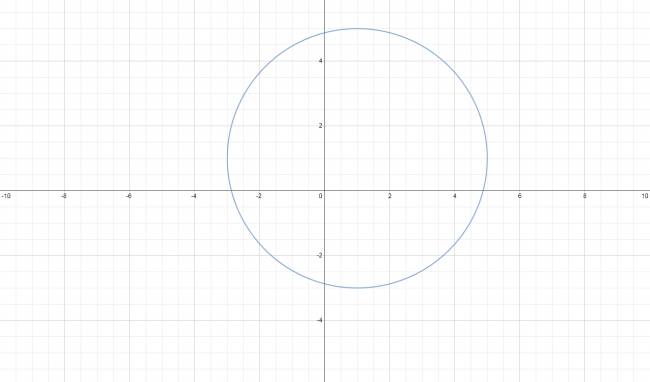
Circunferencia
La ecuación de una cfa es de la forma: $$ x^2 + y^2 + a·x + b·y + c = 0 $$ De todo eso podemos y debemos obtener el centro y el radio, ya que con esos datos ya la podemos graficar. · El centro se puede calcular como: $$ C \left ( -\frac {a}{2}, -\frac {b}{2} \right ) $$ · El radio se puede calcular como: $$ r^2 = \frac {a^2 + b^2 - 4·c^2}{4} ⇒ r = \frac {1}{2}·\sqrt {a^2 + b^2 - 4·c^2} $$ Un ejemplo para entender más: ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |