|
| Foro Departamento de Matemática Teóricos Valor absoluto o módulo |
| Valor absoluto o módulo |
|
03-04-2013, 10:38 PM
Post: #1
|
|||
|
|||
|
Valor absoluto o módulo
Definición: $$ |x| = \begin{cases} x, \mbox{ si } x≥0 \\ -x, \mbox{ si } x <0 \end{cases} $$ O sea, consiste en escribir un número siempre como positivo. Ejemplos: $$ |-8| = 8 $$ $$ |2| = 2 $$ $$ |0| = 0 $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
05-04-2013, 6:34 PM
Post: #2
|
|||
|
|||
|
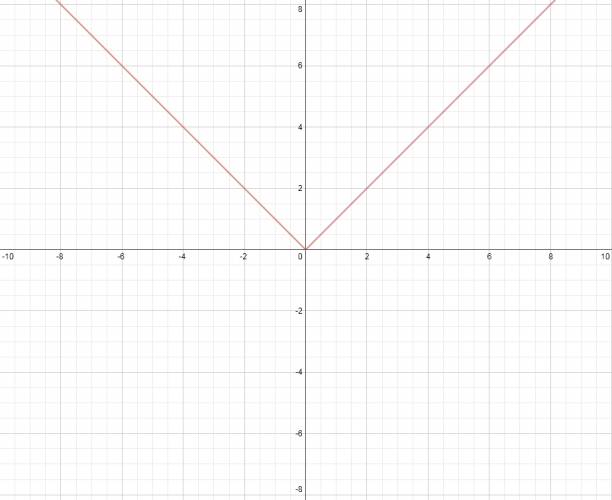
Función valor absoluto o módulo
$$ f:ℝ → ℝ_{0}^{+} $$ O sea, es una función cuyo dominio es el conjunto de los números reales, y su codominio es el conjunto de los números reales positivos y el cero, o sea, todos los números reales que no sean negativos. Forma general: $$ f(x) = |x| $$ Gráfico: $$ f(x) = |x| $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
18-04-2013, 0:13 AM
Post: #3
|
|||
|
|||
|
Propiedades:
· No-negatividad: $$ |x| ≥ 0, ∀x∈ℝ $$ $$ |x| = 0 ⇔ x = 0 $$ · Desigualdad triangular: $$ |x + y| ≤ |x| + |y| $$ · Igualdad multiplicativa: $$ |x·y| = |x|·|y| $$ · Igualdad del cociente: $$ \left | \frac {x}{y} \right | = \frac {|x|}{|y|}, ∀x∈ℝ, ∀y∈ℝ^{*} $$ ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
09-12-2013, 5:35 PM
Post: #4
|
|||
|
|||
|
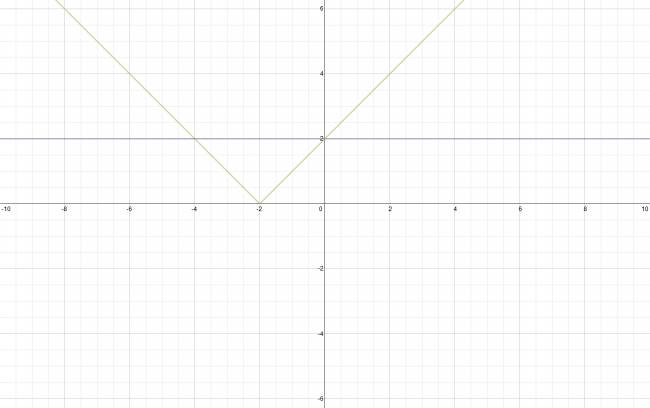
Resolución de ecuaciones en valor absoluto
Método analítico: Introducción: Sabemos que si: \( |x| = 1 \), habrán dos valores de \( x \) que verifican esta igualdad. Uno de ellos es cuando \( x = 1 \) y el otro es cuando \( x = -1 \). Esta simple ecuación, la pudimos haber resuelto mentalmente debido a una sencillez, pero intentemos razonar cómo la resolvimos, para luego aplicar el mismo razonamiento a ecuaciones más complejas. Las barras de valor absoluto hacen que cualquier número se escriba como positivo. Esto quiere decir que un número positivo, se escribirá como el mismo número. Pero el opuesto de éste (un número negativo) se escribirá, también, como un número positivo. De aquí sacamos que el resultado siempre es un número positivo, pero lo que está adentro de las barras de valor absoluto no siempre lo será. Por esta razón, es necesario suponer que lo que se encuentra dentro de las barras es positivo y negativo. Ahora, volvamos a la ecuación que planteamos más arriba. Podemos afirmar lo siguiente: $$ |x| = 1 ⇔ x = 1 ∨ -x= 1 $$ Como vemos, hemos llegado a dos ecuaciones simples de primer grado, donde las soluciones son simples de calcular. Vamos a sacar en limpio lo que hicimos: 1. Consideramos como positivo o cero lo que se encuentra dentro de las barras de valor absoluto y resolvemos la ecuación que nos quedó. 2. Consideramos como negativo lo que se encuentra dentro de las barras de valor absoluto y resolvemos la ecuación que nos quedó. 3. El conjunto solución, fue la unión de los anteriores conjunto de solución de cada ecuación. Ahora consideremos una ecuación algo más difícil: $$ |x+3| = 2·x $$ Si aplicamos el razonamiento de más arriba, llegamos a lo siguiente: $$ |x+3| = 2·x ⇔ x+3 = 2·x ∨ -(x+3) = 2·x $$ Por lo que las soluciones serían: \( x = 3 ∨ x = 1 \) Si verificamos el conjunto solución, vemos que \( x = 3 \) es solución de la ecuación, pero que \( x = 1 \) no lo es. La pregunta que nos podemos plantear es: ¿cómo podemos hacer para que nos den las raíces de la ecuaciones y no otros números más? Esto se puede resolver aplicando razonamientos un poco más abstractos. Si consideramos que lo que está dentro de las barras de valor absoluto es positivo o cero, no deberíamos de permitir que nos dé un número negativo. Por esta razón debemos aplicar la idea de dominio. El dominio no es otra cosa que el conjunto de todos los valores de \( x \) que tienen una correspondiente imagen. El dominio sólo nos interesará en las expresiones que se encuentren dentro de las barras de valor absoluto, ya que serán las que tienen un comportamiento extraño en relación a las ecuaciones polinómicas que se venían trabajando. Vamos a sacar en limpio la idea: 1. Consideramos como positivo o cero lo que se encuentra dentro de las barras de valor absoluto y resolvemos la ecuación que nos quedó. Estudiamos el dominio (resolvemos la siguiente inecuación: \( f(x) ≥ 0 \), siendo \( f(x) \) la expresión que se encuentra dentro de las barras de valor absoluto). Se descartarán todas las soluciones que no pertenezcan al dominio. 2. Consideramos como negativo lo que se encuentra dentro de las barras de valor absoluto y resolvemos la ecuación que nos quedó. Estudiamos el dominio (resolvemos la siguiente inecuación: \( f(x) < 0 \), siendo \( f(x) \) la expresión que se encuentra dentro de las barras de valor absoluto). Se descartarán todas las soluciones que no pertenezcan al dominio. 3. El conjunto solución, fue la unión de los anteriores conjunto de solución de cada ecuación. Para los casos en que hay más de un valor absoluto en la ecuación: Supongamos el caso siguiente, se nos pide resolver la ecuación: $$ |x+2| = |2·x| $$ Aquí habrán cuatro casos a considerar: que ambas expresiones sean positivas o cero, que ambas expresiones sean negativas, que la primera sea positiva o cero y la segunda negativa, que la primera sea negativa y la segunda positiva o cero. La forma en que se resuelve es análoga al anterior caso y no tiene mucha cosa extraña más. Generalización: Aquí vimos el caso de expresiones en barras de valor absoluto que son polinómicas, pero puede haber cualquier cosa dentro de las barras, pero si conocemos las propiedades del valor absoluto y de la otra expresión, se podrá resolver sin mayores dificultades. Método gráfico: Este método es más incómodo, hay que tener instrumentos y ser muy preciso. Acá no se valora tanto el razonamiento sino que dé lo que tiene que dar. Introducción: Supongamos que se nos pide resolver gráficamente la ecuación: \( |x+2| = 2 \). Esto lo haremos a través de conceptos de funciones. Consideraremos las expresiones a ambos miembros, como dos funciones a parte. E.g.: \( q(x) = |x+2| ∧ p(x) = 2 \). \( q(x) \) es una función módulo (valor absoluto), mientras que \( p(x) \) es una función constante (para todo valor de \( x \), su imagen es 2). Ahora lo que se hace, es graficar ambas funciones en el mismo sistema de ejes. Las soluciones serán todos los valores de \( x \) en que se corten ambas funciones. Como vemos, las soluciones de la anterior ecuación son: \( x = -4 ∨ x = 0 \) Para graficar funciones módulo, es muy conveniente estar muy claro con el corrimiento de gráficos. Y hacer una tablita de valores, con tres valores de \( x \) (o más), nunca viene mal, sobretodo si se ignoran demás propiedades de funciones polinómicas de primer grado. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |