|
| Foro Departamento de Matemática Teóricos Ecuación cuadrática |
| Ecuación cuadrática |
|
09-11-2012, 11:02 PM
Post: #1
|
|||
|
|||
|
Una ecuación es cuadrática o una ecuación es de segundo grado, si el máximo exponente al que está elevada la variable es dos, y que todos los exponentes a los que están elevadas las variables sean números naturales.
$$ a·x^2 + b·x + c = 0, ∀(a,b,c)∈ℝ, a≠0 $$ Existen tres tipos de ecuaciones cuadráticas: 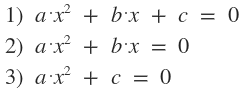 Quote Absolutamente toda ecuación cuadrática tiene dos raíces, puede que sean dos iguales o dos distintas; reales o complejas; pero siempre tienen dos raíces. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
10-11-2012, 3:34 AM
Post: #2
|
|||
|
|||
|
Resolución de ecuaciones cuadráticas:
Fórmula de Bháskara: Existe una fórmula que se le atribuye al matemática indio Bháskara que permite resolver los tres tipos de ecuaciones cuadráticas. Se sustituyen los coeficientes en la siguiente fórmula: $$ x = \frac {- b ± \sqrt {b^2 - 4·a·c}}{2·a} $$ Discriminante: Se representa con la letra delta mayúscula (\( ∆ \)) a todo lo que se encuentra bajo el símbolo de radical, y esto nos permite saber un par de cosas de las raíces de la ecuación. $$ ∆ = b^2 - 4·a·c $$  Otro método para resolver el tercer tipo de ecuaciones cuadráticas: Por simple despeje: 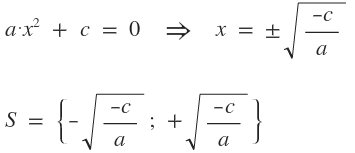 Otro método para resolver el segundo tipo de ecuaciones cuadráticas: Se factoriza (se saca de factor común la x) y se aplica la propiedad Hankeliana (si el producto de dos números es cero es porque algunos de ellos lo es): 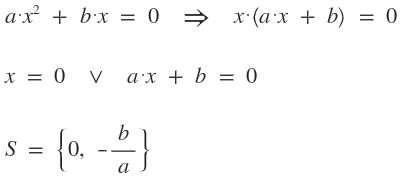 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
24-01-2013, 10:23 PM
Post: #3
|
|||
|
|||
|
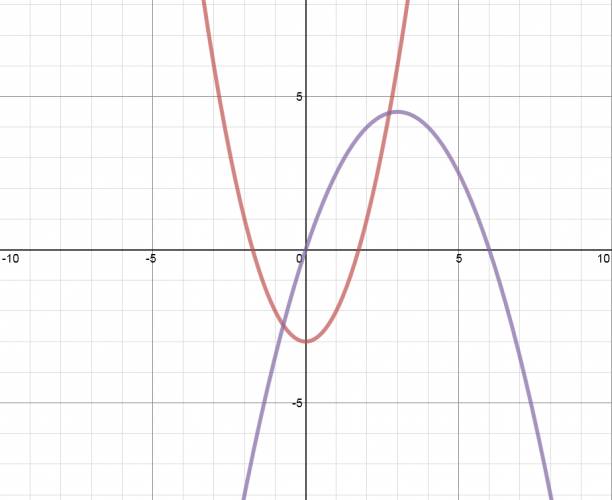
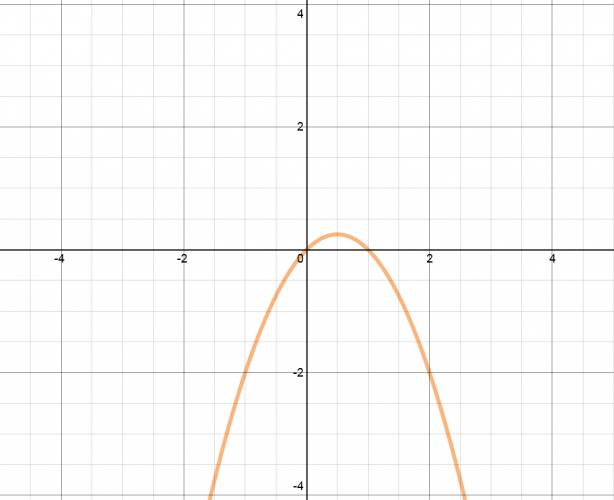
Función cuadrática:
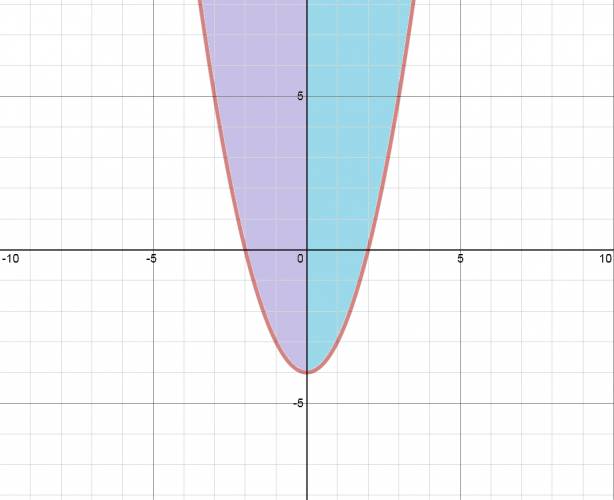
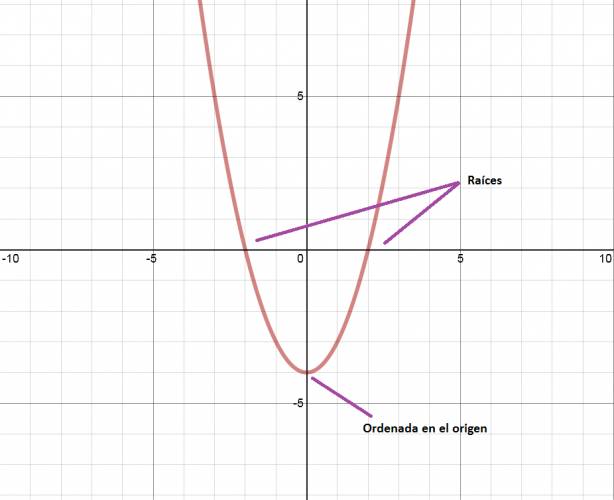
· Forma polinómica: \( f(x) = a·x^2 + b·x + c \) Ejemplo: \( f(x) = x^2 + x - 6 \) · Forma factorizada: \( f(x) = a·(x - \alpha)·(x - \beta) \) Siendo: · \( a \) = término principal. · \( x \) = variable de la ecuación. · \( \alpha \) = una de las raíces. · \( \beta \) = otra de las raíces. Ejemplo: \( f(x) = (x-2)·(x+3) \) · Forma canónica: \( f(x) = a·( x - x_{v} )^2 + y_{v} \) Cálculo de \( x_{v} \): \(x_{v} = \frac {\alpha + \beta}{2} = \frac{-b}{2·a} \) O también se puede hallar como la semisuma de las raíces: \( x_{v} = \frac {\alpha + \beta}{2} \) Siendo \( \alpha \) y \( \beta \) las raíces de la función. Cálculo de \( y_{v} \): Se hace conociendo de antemano \( x_{v} \). Se sustituye la variable \( x \) por el valor de \( x_{v} \), y el resultado es \( y_{v} \). \( f( x_{v} ) = a·x_{v}^2 + b·x_{v} + c \) O también se puede hallar a través de la fórmula: \( y_{v} = \frac {4·a·c - b^2}{4·a} \) Vértice de la parábola: \( v (x_{v}, y_{v}) \) Ejemplo: \( f(x) = (x + \frac{1}{2})^2 - \frac{25}{4} \) Quote Se escribió el mismo polinomio en las tres formas distintas. Todas las formas son equivalentes, tienen el mismo conjunto solución, es la misma función escrita de otra manera. Las funciones cuadráticas son de la forma: Que reciben el nombre de parábola. La parábola tiene un eje de simetría, por lo tanto, el área violeta es igual al área celeste: El eje de simetría de la parábola pasa por el vértice de esta. Análisis de la función: De un gráfico se pueden deducir varias cosas, por ejemplo: la raíz o las raíces, la ordenada en el origen, etc. Deducción del gráfico: Conjunto solución: \( S = \left\{ -2, +2 \right\} \) Ordenada en el origen: \( -4 \) Concavidad: La concavidad de la función depende del signo que posea el coeficiente principal: Quote · Si el coeficiente principal es positivo la función tendrá concavidad positiva. Recordar cara feliz  · Si el coeficiente principal es negativo la función tendrá concavidad negativa. Recordar cara triste  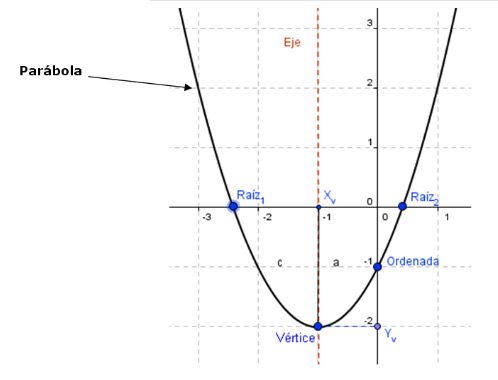 ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
|
24-01-2013, 10:30 PM
Post: #4
|
|||
|
|||
|
Relaciones entre raíces y coeficientes
$$ a·x^2 + b·x + c = 0 $$ La relación entre los coeficientes y las raíces en los polinomios cuadráticos se suele expresar de la siguiente manera: $$ a·x^2 - S·x + P = 0 $$ Siendo: · S = suma de las raíces · P = producto de las raíces $$ \left \{ \begin{array}{rcl} \alpha + \beta = - \frac {b}{a} \\ \alpha · \beta = \frac {c}{a} \end{array} \right . $$ Siendo: · \( \alpha \) = una raíz del polinomio. · \( \beta \) = otra raíz del polinomio. ¿No estás de acuerdo con lo que escribí? ¡por favor explícame tu punto de vista! :) · No se resuelven problemas ni se responde a consultas sobre matemática, física ni química por mensaje privado. · Si utilizas material de este sitio, no olvides citar la fuente. · Si te sirvió lo que dije, puedes agradecerme aumentado mi reputación. · Si ven que tengo una falta de ortografía un hechicero lo hizo. |
|||
| |||
| |||
| Últimos cinco temas activos... | |||||
| Tema | Foro | Autor | Respuestas | Último mensaje | |
 | PENDIENTE Ejercicios sobre la ley de Snell (refracción) | Problemas sin resolver | marcos364 | 3 | 19-11-2019 3:52 AM Último mensaje: jaztallica |
 | Saludos a todos | Presentaciones | JOHN | 2 | 29-11-2017 10:20 PM Último mensaje: brunoosorioalmanzar |
 | PENDIENTE Ecuacion circunferencias | Problemas sin resolver | elva | 1 | 08-03-2016 2:06 AM Último mensaje: Admin |
 | Geometría analítica en el plano: circunferencia | Teóricos | Admin | 4 | 18-11-2015 10:57 PM Último mensaje: joserodriguez0173 |
 | PENDIENTE Problema de dinamica, cañón unido a resorte | Problemas sin resolver | andremn | 1 | 14-11-2015 3:18 PM Último mensaje: jotazone10 |