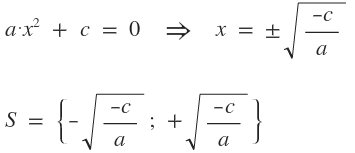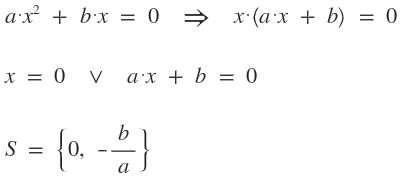09-11-2012, 11:02 PM
Una ecuación es cuadrática o una ecuación es de segundo grado, si el máximo exponente al que está elevada la variable es dos, y que todos los exponentes a los que están elevadas las variables sean números naturales.
$$ a·x^2 + b·x + c = 0, ∀(a,b,c)∈ℝ, a≠0 $$
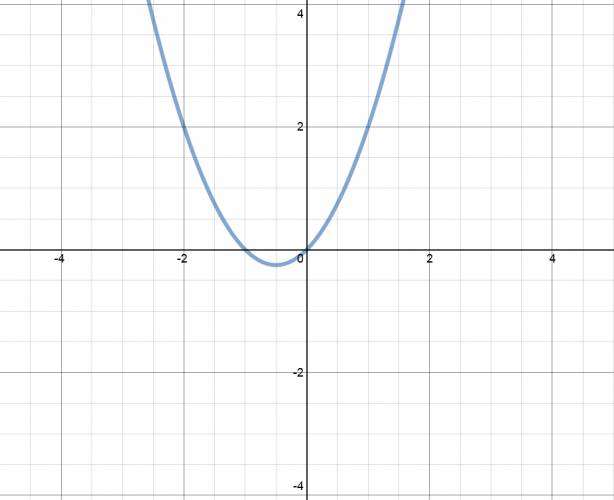
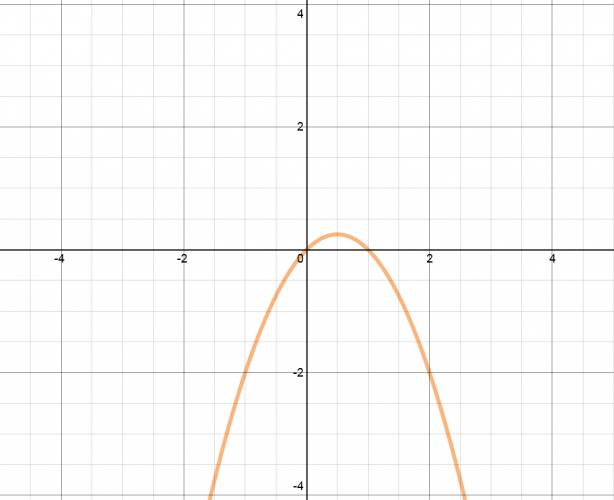
Existen tres tipos de ecuaciones cuadráticas:
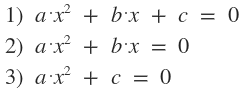
$$ a·x^2 + b·x + c = 0, ∀(a,b,c)∈ℝ, a≠0 $$
Existen tres tipos de ecuaciones cuadráticas:
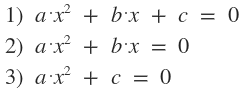
Quote
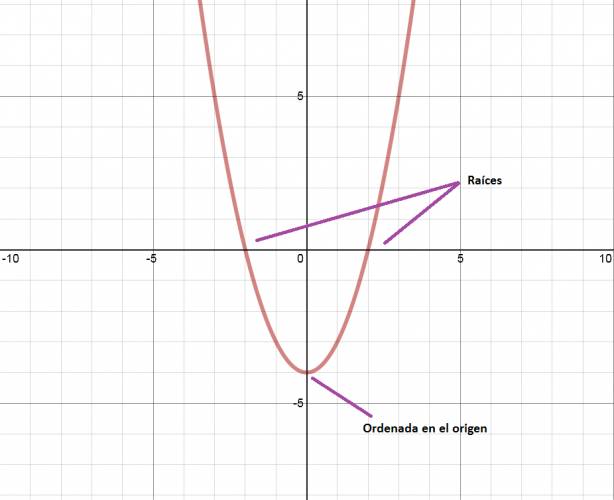
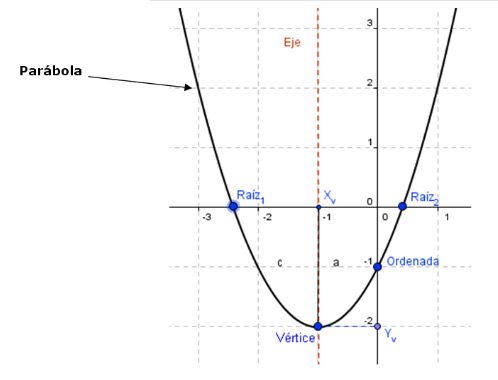
Absolutamente toda ecuación cuadrática tiene dos raíces, puede que sean dos iguales o dos distintas; reales o complejas; pero siempre tienen dos raíces.